题目内容
14.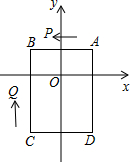 如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).
如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).
分析 由点A、B、C、D的坐标可得出AB、BC的长度,设点P和点Q第2017次相遇时的时间为x,根据路程=速度和×时间,即可得出关于x的一元一次方程,解之即可得出x的值,再根据路程=速度×时间可求出P和点Q第2017次相遇时,点P走过的路程,结合矩形的周长为10,即可找出点P和点Q第2017次相遇时的坐标,此题得解.
解答 解:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),
∴AB=2,BC=3.
设点P和点Q第2017次相遇时的时间为x,
根据题意得:(2+3)x=(2017-1)×2×(2+3)+2+3,
解得:x=4033,
∴P和点Q第2017次相遇时,点P走过的路程为2x=8066.
∵矩形ABCD的周长为10,8066=806×10+6,
∴P和点Q第2017次相遇时的位置在距离点A逆时针方向的6个单位长度.
∵AB+BC=5,CD=2,
∴点P和点Q第2017次相遇时的位置为线段CD的中点,即点(0,-2).
故答案为:(0,-2).
点评 本题考查了规律型中点的坐标、矩形的周长以及一元一次方程的应用,根据点P走过的总路程结合矩形的周长找出点P和点Q第2017次相遇时的位置是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
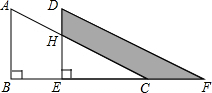 如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4.
如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4. 如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.
如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.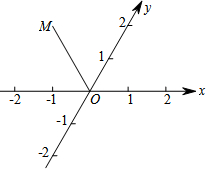 在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )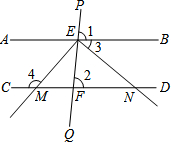 已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.
已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.