��Ŀ����
16�������Ķ�������ϲ�������⣺��һ�κ���y=kx+b��k��0���У��ɰ����²�����Σ�
��kx=y-b��
��x=$\frac{1}{k}$y-$\frac{b}{k}$��k��0����
�۰�x=$\frac{1}{k}$y-$\frac{b}{k}$�е�x��y�������õ�y=$\frac{1}{k}$x-$\frac{b}{k}$��
��ʱ���ǾͰѺ���y=$\frac{1}{k}$x-$\frac{b}{k}$��k��0����������y=kx+b�ķ�������
�ر�أ����������������ʽ��ͬ���Ա�����ȡֵ��ΧҲ��ͬ���������������Ϊͬһ������
��1������y=$\frac{1}{2}$x+1�����ķ������Ľ������ꣻ
��2��������y=kx+2�����ķ�������ͬһ��������k��ֵ��
���� ��1�����ݷ������������ֱ��y=$\frac{1}{2}$x+1�ķ�����Ϊy=2x-2���������������ɵã�
��2�����������y=kx+2�ķ�����Ϊy=$\frac{1}{k}$x-$\frac{2}{k}$������������Ϊͬһ�����ɵ�k��ֵ��
��� �⣺��1����y=$\frac{1}{2}$x+1��
��y-1=$\frac{1}{2}$x��
2y-2=x��
��y=$\frac{1}{2}$x+1�ķ�����Ϊy=2x-2��
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=2x-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$��
�ຯ��y=$\frac{1}{2}$x+1�����ķ������Ľ�������Ϊ��2��2����
��2����y=kx+2��
��kx=y-2��
x=$\frac{1}{k}$y-$\frac{2}{k}$��
��y=kx+2�ķ�����Ϊy=$\frac{1}{k}$x-$\frac{2}{k}$��
�ߺ���y=kx+2�����ķ�������ͬһ������
��$\left\{\begin{array}{l}{\frac{1}{k}=k}\\{-\frac{2}{k}=2}\end{array}\right.$��
��ã�k=-1��
���� ������Ҫ���鷴����������һ�κ����������⣬�����¶���ó��������Ľ���ʽ�����������ֱ�߽����ǽ���Ĺؼ���

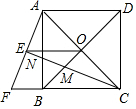 ��ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ӳ�CB����F��ʹCF=CA������AF����ACF��ƽ���߷ֱ�AF��AB��BD�ڵ�E��N��M������EO����֪BD=2$\sqrt{2}$��
��ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ӳ�CB����F��ʹCF=CA������AF����ACF��ƽ���߷ֱ�AF��AB��BD�ڵ�E��N��M������EO����֪BD=2$\sqrt{2}$��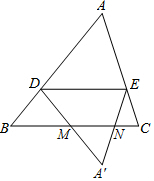 ��ͼ���ڡ�ABC�У���D�ڱ�AB�ϣ�����A��B�غϣ���DE��BC��AC�ڵ�E������ADE��ֱ��DE���ۣ��õ���A��DE��ֱ��DA�䣬EA��ֱ�ֱ��BC�ڵ�M��N��
��ͼ���ڡ�ABC�У���D�ڱ�AB�ϣ�����A��B�غϣ���DE��BC��AC�ڵ�E������ADE��ֱ��DE���ۣ��õ���A��DE��ֱ��DA�䣬EA��ֱ�ֱ��BC�ڵ�M��N�� ��ͼ����֪E��F��G��H�ֱ��Ǿ����ı�AB��BC��CD��DA���е㣬���ı���EFGH���ܳ�Ϊ16cm�������ABCD�ĶԽ��߳�����8cm��
��ͼ����֪E��F��G��H�ֱ��Ǿ����ı�AB��BC��CD��DA���е㣬���ı���EFGH���ܳ�Ϊ16cm�������ABCD�ĶԽ��߳�����8cm��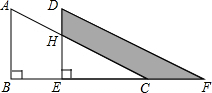 ��ͼ��ֱ�ǡ�ABC�ص�B����C�ķ���ƽ�Ƶ���DEF��λ�ã���AB=5��DH=1��ƽ�ƾ���Ϊ2������Ӱ����DHCF���������4��
��ͼ��ֱ�ǡ�ABC�ص�B����C�ķ���ƽ�Ƶ���DEF��λ�ã���AB=5��DH=1��ƽ�ƾ���Ϊ2������Ӱ����DHCF���������4��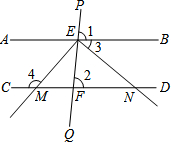 ��֪����ͼ��ֱ��PQ�ֱ���ֱ��AB��CD���ڵ�E�͵�F����1=��2������EM��EN�ֱ���ֱ��CD���ڵ�M��N����EM��EN����3=40�㣬���4�Ķ�����
��֪����ͼ��ֱ��PQ�ֱ���ֱ��AB��CD���ڵ�E�͵�F����1=��2������EM��EN�ֱ���ֱ��CD���ڵ�M��N����EM��EN����3=40�㣬���4�Ķ�����