题目内容
11. 如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标.
如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标.
分析 如图,过点A作AH⊥x轴于点H,过点D作作DF⊥x轴于点F.由反比例函数图象上点的坐标特征、等边三角形的性质和三角形的面积公式进行解答.
解答  解:如图,过点A作AH⊥x轴于点H,过点D作作DF⊥x轴于点F.
解:如图,过点A作AH⊥x轴于点H,过点D作作DF⊥x轴于点F.
∵△AOC为等边三角形,
∴设A(a,$\sqrt{3}$a),
又∵点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,
∴$\sqrt{3}$a2=$\sqrt{3}$,
解得a=1(舍去负值).
则A(1,$\sqrt{3}$).
同理,设D(b,$\sqrt{3}$(b-2)).
则$\sqrt{3}$b(b-2)=$\sqrt{3}$,
解得b=$\sqrt{2}$+1(舍去负值).
则D($\sqrt{2}$+1,$\sqrt{6}$-$\sqrt{3}$).
点评 本题考查了反比例函数图象上点的坐标特征,利用了等腰三角形的性质,待定系数法求函数解析式,函数图象上的点的坐标满足函数解析式.

练习册系列答案
相关题目
 如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.
如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数. 如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.
如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.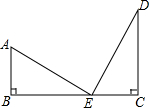 如图,有两根直杆AB,CD隔河相对,AB高20m,CD高30m,两杆相距50m,现两杆杆顶上各有一只鱼鹰,它们同时看到两杆之间河面上E处浮起的一条小鱼,于是以同样的速度同时飞下来争夺该鱼,结果两只鱼鹰同时到达,叼住小鱼,两杆杆底到E处的水平距离各是多少米?
如图,有两根直杆AB,CD隔河相对,AB高20m,CD高30m,两杆相距50m,现两杆杆顶上各有一只鱼鹰,它们同时看到两杆之间河面上E处浮起的一条小鱼,于是以同样的速度同时飞下来争夺该鱼,结果两只鱼鹰同时到达,叼住小鱼,两杆杆底到E处的水平距离各是多少米? 如图,DE∥BC,AD:DB=3:5,则△ADE与△ABC的面积之比为9:64.
如图,DE∥BC,AD:DB=3:5,则△ADE与△ABC的面积之比为9:64.