题目内容
19. 如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.
如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.
分析 连接CM,首先证明∠ACB=90°,根据直角三角形斜边上的中线等于斜边的一半可得CM=$\frac{1}{2}AB$=AM,进而可证明△ACM是等边三角形,再根据等腰三角形三线合一的性质可得DM=$\frac{1}{2}$AM,进而可得结论.
解答  证明:连接CM,
证明:连接CM,
∵∠A=2∠B=60°,
∴∠B=30°,
∴∠ACB=90°,
∵点M是AB的中点,
∴CM=$\frac{1}{2}AB$=AM,
∴△ACM是等边三角形,
∵CD⊥AB,
∴DM=$\frac{1}{2}$AM,
∴2DM=AC.
点评 此题主要考查了等边三角形的判定和性质,以及直角三角形的性质,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
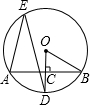 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB=10$\sqrt{3}$.
如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=30°,OB=10,则弦AB=10$\sqrt{3}$. 如图,?ABCD的边BC长为6,中点为原点,AB长为2,∠ABC=60°,求它的四个顶点的坐标.
如图,?ABCD的边BC长为6,中点为原点,AB长为2,∠ABC=60°,求它的四个顶点的坐标. 如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标.
如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标. 如图,在△ABC中,AD⊥BC于D,EF⊥BC于F,BE交AD于G,EF是∠BEC的角平分线,证明:∠EAG=∠AGE.
如图,在△ABC中,AD⊥BC于D,EF⊥BC于F,BE交AD于G,EF是∠BEC的角平分线,证明:∠EAG=∠AGE.