题目内容
6．已知?ABCD的周长为40，对角线AC，BD相交于点O，△AOB的周长比△BOC的周长大6，则AB=13，BC=7．分析 根据平行四边形对边相等可得BC+AB=20，根据△AOB的周长比△BOC的周长大6可得AB-BC=6，组成方程组，再解即可．
解答 解：∵平行四边形的周长为40，
∴BC+AB=20；
∵△AOB的周长比△BOC的周长大6，
∴AB-BC=6，
$\left\{\begin{array}{l}{CB+AB=20}\\{AB-BC=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{AB=13}\\{BC=7}\end{array}\right.$，
故答案为：13；7．
点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形两组对边分别相等，对角线互相平分．
练习册系列答案
口算题天天练系列答案
相关题目
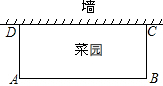用一段长为20米的篱笆围成一个一边靠墙（墙的长度不限）的矩形花圃ABCD，设AB边长为x米，求花圃的面积y与x的函数关系式并写出自变量x的取值范围．
超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市收银台排队付款的等待时间，并绘制成如图所示的频数分布直方图（图中等待时间0分钟到1分钟表示大于或等于0分钟而小于1分钟，其他类同）．这个时间段内顾客等待时间不少于6分钟的人数为7．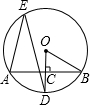
如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，点E在⊙O上，∠AED=30°，OB=10，则弦AB=10$\sqrt{3}$．
如图，△AOC与△DCE均为等边三角形，点A、D在双曲线y=$\frac{\sqrt{3}}{x}$（x＞0）上，点O为坐标原点，点C、E在x轴上，求点A、D的坐标．
15．函数y=x2+kx+1与y=x2-x-k的图象相交，若有一个交点在x轴上，则k的值为（ ）
| A． | 0 | B． | -1 | C． | 2 | D． | $\frac{1}{4}$ |