题目内容
1. 如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.
如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.
分析 设∠EBD=x,根据等边对等角表示出∠BDE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AED,然后表示出∠A,再利用三角形的一个外角等于与它不相邻的两个内角的和表示出∠BDC,然后表示出∠C、∠CBD,最后利用三角形的内角和等于180°列方程求出x,再求解即可.
解答 解:设∠EBD=x,
∵DE=BE,
∴∠BDE=∠EBD=x,
在△BED中,∠AED=∠EBD+∠BDE=x+x=2x,
∵AD=DE,
∴∠A=∠AED=2x,
在△ABD中,∠BDC=∠EBD+∠A=x+2x=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
∴∠CBD=∠ABC-∠EBD=3x-x=2x,
在△BCD中,∠CBD+∠C+∠BDC=180°,
即2x+3x+3x=180°,
解得x=22.5°.
所以∠A=2x=2×22.5°=45°.
点评 本题考查了等腰三角形的性质,三角形的内角和定理,利用等边对等角表示出各角度并最后列出方程是解题的关键.

练习册系列答案
相关题目
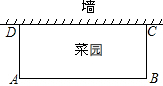 用一段长为20米的篱笆围成一个一边靠墙(墙的长度不限)的矩形花圃ABCD,设AB边长为x米,求花圃的面积y与x的函数关系式并写出自变量x的取值范围.
用一段长为20米的篱笆围成一个一边靠墙(墙的长度不限)的矩形花圃ABCD,设AB边长为x米,求花圃的面积y与x的函数关系式并写出自变量x的取值范围.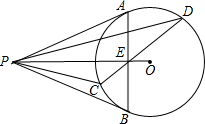 如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD.
如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD. 如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标.
如图,△AOC与△DCE均为等边三角形,点A、D在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,点O为坐标原点,点C、E在x轴上,求点A、D的坐标.