题目内容
14. 如图,△ABC中,D、E、F、G分别为BC、BD、AB、FB的中点,若S△ABC=32,求S△BEG.
如图,△ABC中,D、E、F、G分别为BC、BD、AB、FB的中点,若S△ABC=32,求S△BEG.
分析 根据D、E、F、G分别为BC、BD、AB、FB的中点,于是得到$\frac{BE}{BC}=\frac{1}{4}$,$\frac{BG}{AB}$=$\frac{1}{4}$,推出EG∥AC,证得△BEG∽△BCA,然后根据相似三角形的性质即可得到结论.
解答 解:∵D、E、F、G分别为BC、BD、AB、FB的中点,
∴$\frac{BE}{BC}=\frac{1}{4}$,$\frac{BG}{AB}$=$\frac{1}{4}$,
∴$\frac{BE}{BC}=\frac{BG}{AB}$,
∴EG∥AC,
∴△BEG∽△BCA,
∴$\frac{{S}_{△BEG}}{{S}_{△BCA}}$=($\frac{BE}{BC}$)2=$\frac{1}{16}$,
∵S△ABC=32,
∴S△BEG=2.
点评 本题考查了相似三角形的判定和性质,三角形的面积,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
4.已知二次函数y=ax2+bx+c的y与x部分对应值如下表:
则下列判断中正确的是( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于负半轴 | ||
| C. | 物线的对称轴为x=1 | D. | 当x=4时,y<0 |
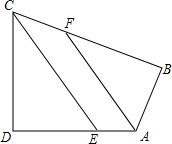 如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B.
如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B. 如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少? 将如图所示的围棋盘放在平面直角坐标系内,黑棋A的坐标为(-1.2),黑棋C的坐标为(1,1),那么白棋B的坐标为(-3,-2).
将如图所示的围棋盘放在平面直角坐标系内,黑棋A的坐标为(-1.2),黑棋C的坐标为(1,1),那么白棋B的坐标为(-3,-2).