题目内容
14. 如图,在?ABCD中,E、F是DB上两点,且BF=DE,若∠AEB=115°,∠ADB=30°,求∠BCF的度数.
如图,在?ABCD中,E、F是DB上两点,且BF=DE,若∠AEB=115°,∠ADB=30°,求∠BCF的度数.
分析 由AB=DC,AD=BC可知四边形ABCD为平行四边形,根据BF=DE,可证△ADE≌△CBF,则∠BCF=∠DAE,因为∠AEB=115°、∠ADB=30°,所以可推得∠BCF=85°.
解答 解:∵四边形ABCD为平行四边形,
∴AB=DC,AD=BC,∠ADE=∠CBF,
在△ADE与△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠ADE=∠CBF}\\{BF=DE}\end{array}\right.$,
∴△ADE≌△CBF,
∴∠BCF=∠DAE,
∵∠DAE=180°-∠ADB-∠AED,
∵∠AED=180°-∠AEB=65°,∠ADB=30°,
∴∠BCF=∠DAE=85°.
点评 本题主要考查了平行四边形的性质,运用平行四边形的性质解决以下问题,如求角的度数、线段的长度,证明角相等或互补,证明线段相等或倍分等.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
5.一个直角三角形的两条直角边分别是2cm,$\sqrt{2}$cm,那么它的斜边长是( )
| A. | $\sqrt{2}$cm | B. | 2$\sqrt{2}$cm | C. | $\sqrt{3}$cm | D. | $\sqrt{6}$cm |
2.a2=1,b是2的相反数,则a+b的值为( )
| A. | -3 | B. | -1 | C. | -1或-3 | D. | 1或-3 |
19.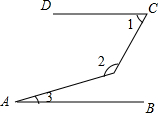 如图,已知AB∥CD,则∠1、∠2和∠3之间的关系为( )
如图,已知AB∥CD,则∠1、∠2和∠3之间的关系为( )
 如图,已知AB∥CD,则∠1、∠2和∠3之间的关系为( )
如图,已知AB∥CD,则∠1、∠2和∠3之间的关系为( )| A. | ∠2+∠1-∠3=180° | B. | ∠3+∠1=∠2 | C. | ∠3+∠2+∠1=360° | D. | ∠3+∠2-2∠1=180° |
6.已知不等式组$\left\{\begin{array}{l}{x-3>0}\\{x+1≥0}\end{array}\right.$,其解集正确的是( )
| A. | -1≤x<3 | B. | -1<x≤3 | C. | x>3 | D. | x≤-1 |
3.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如表:某同学分析表后得出如下结论:
(1)甲、乙两班学生成绩平均水平相同;
(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
(3)甲班成绩的波动比乙班小.上述结论正确的是( )
| 班级 | 人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
(3)甲班成绩的波动比乙班小.上述结论正确的是( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |