题目内容
5.一个直角三角形的两条直角边分别是2cm,$\sqrt{2}$cm,那么它的斜边长是( )| A. | $\sqrt{2}$cm | B. | 2$\sqrt{2}$cm | C. | $\sqrt{3}$cm | D. | $\sqrt{6}$cm |
分析 根据勾股定理计算即可.
解答 解:直角三角形的斜边长=$\sqrt{{2}^{2}+(\sqrt{2})^{2}}$=$\sqrt{6}$,
故选:D.
点评 本题考查的是勾股定理的应用,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
16.某超市要进一批鸡蛋进行销售,有A,B两家农场可供货.为了解两家提供的鸡蛋单个大小,超市分别对A,B两农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
(1)下列抽样方式中比较合理的是哪一种?
①分别从A,B两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋分别称出其每个鸡蛋的质量;
②分别从A,B两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋分别称出其每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量,结果如下表(单位:g,数据包括左端点不包括右端点):
①如果从这两家农场提供的鸡蛋中随机拿一个,分别估计两家鸡蛋质量在50±3 (单位:g)范围内的概率;
②如果你是超市经营者,请你通过数据分析,确定选择哪家农场提供的鸡蛋.
(1)下列抽样方式中比较合理的是哪一种?
①分别从A,B两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋分别称出其每个鸡蛋的质量;
②分别从A,B两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋分别称出其每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量,结果如下表(单位:g,数据包括左端点不包括右端点):
| 45-47 | 47-49 | 49-51 | 51-53 | 53-55 | |
| A农场鸡蛋 | 2 | 8 | 15 | 10 | 5 |
| B农场鸡蛋 | 4 | 6 | 12 | 14 | 4 |
②如果你是超市经营者,请你通过数据分析,确定选择哪家农场提供的鸡蛋.
15.如果x>y,那么下列不等式中不成立的是( )
| A. | x+3>y+3 | B. | -1+x>-1+y | C. | $\frac{x}{2}$>$\frac{y}{2}$ | D. | -3x>-3y |

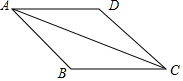 已知:如图,∠BAD=∠DCB,∠BAC=∠DCA.
已知:如图,∠BAD=∠DCB,∠BAC=∠DCA.
 如图,在?ABCD中,E、F是DB上两点,且BF=DE,若∠AEB=115°,∠ADB=30°,求∠BCF的度数.
如图,在?ABCD中,E、F是DB上两点,且BF=DE,若∠AEB=115°,∠ADB=30°,求∠BCF的度数.