题目内容
 如图,已知在△ABC中,AB=AC,AD⊥BC,垂足为D,试用(HL)全等识别法说明AD平分∠BAC.
如图,已知在△ABC中,AB=AC,AD⊥BC,垂足为D,试用(HL)全等识别法说明AD平分∠BAC.考点:全等三角形的判定与性质,等腰三角形的性质
专题:常规题型
分析:由AD⊥BC,可得∠ADB=∠ADC=90°,从而得到两个直角三角形Rt△ADB和Rt△ADC,然后由AB=AC,AD=AD,根据HL定理可判定Rt△ADB≌Rt△ADC,由全等三角形的对应角相等,得出∠BAD=∠CAD,所以AD平分∠BAC.
解答: 证明:∵AD⊥BC,
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°(垂直的定义),
∴△ABD和△ACD都是Rt△,
在Rt△ADB和Rt△ADC中
∵
,
∴Rt△ADB≌Rt△ADC(HL),
∴∠BAD=∠CAD(全等三角形的对应角相等),
∴AD平分∠BAC(角平分线的定义).
 证明:∵AD⊥BC,
证明:∵AD⊥BC,∴∠ADB=∠ADC=90°(垂直的定义),
∴△ABD和△ACD都是Rt△,
在Rt△ADB和Rt△ADC中
∵
|
∴Rt△ADB≌Rt△ADC(HL),
∴∠BAD=∠CAD(全等三角形的对应角相等),
∴AD平分∠BAC(角平分线的定义).
点评:此题考查了利用“HL”定理判定两个直角三角形全等,及由全等三角形的对应角相等,得出结论.

练习册系列答案
相关题目
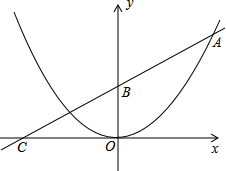 如图已知二次函数图象的顶点为原点,直线y=
如图已知二次函数图象的顶点为原点,直线y= 如图,AB是的直径长为20cm,弦AC为12cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
如图,AB是的直径长为20cm,弦AC为12cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.