题目内容
求证:方程(a-b)x2+(b-c)x+c-a=0有一个根为1.
考点:一元二次方程的解,一元一次方程的定义
专题:证明题
分析:分类讨论:当a-b=0,解一次方程得到x=1;当a-b≠0,当x=1时,计算出方程左边=右边,根据一元二次方程解的定义得到x=1是方程(a-b)x2+(b-c)x+c-a=0的一个根.
解答:证明:当a-b=0,即a=b,则方程方程化为(a-c)x+c-a=0,解得x=1;
当a≠b,把x=1代入方程左边得左边=a-b+b-c+c-a=0,则左边代入右边,所以x=1是方程的解,
所以方程(a-b)x2+(b-c)x+c-a=0有一个根为1.
当a≠b,把x=1代入方程左边得左边=a-b+b-c+c-a=0,则左边代入右边,所以x=1是方程的解,
所以方程(a-b)x2+(b-c)x+c-a=0有一个根为1.
点评:本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了一元二次方程的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图,可计算出该月食堂午餐盒饭的平均价格是
某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图,可计算出该月食堂午餐盒饭的平均价格是 如图,已知在△ABC中,AB=AC,AD⊥BC,垂足为D,试用(HL)全等识别法说明AD平分∠BAC.
如图,已知在△ABC中,AB=AC,AD⊥BC,垂足为D,试用(HL)全等识别法说明AD平分∠BAC.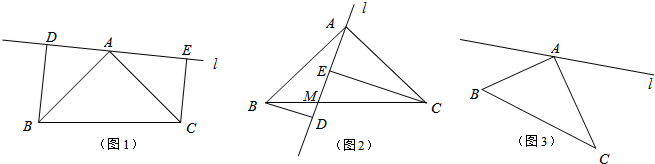
 如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.
如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.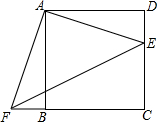 如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.