Question

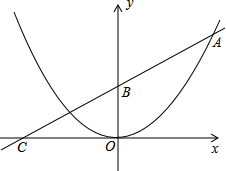如图已知二次函数图象的顶点为原点，直线y=

1

2

x+4的图象与该二次函数的图象交于A点（8，8），直线与x轴的交点为C，与y轴的交点为B．求这个二次函数的解析式与B点坐标．

Answer 1

考点：抛物线与x轴的交点

专题：

分析：由已知条件可设二次函数的解析式为y=ax²（a≠0），把A（8，8）代入即可求得a的值进而求得二次函数的解析式，根据直线的解析式令x=0，即可求得纵坐标，进而求得B的坐标．

解答：解：∵二次函数图象的顶点为原点，
∴设二次函数的解析式为y=ax²（a≠0），
把A（8，8）代入得：8=64a，
解得：a=

1

8

．
∴二次函数的解析式为y=

1

8

x²；
∵直线y=

1

2

x+4与y轴的交点为B．
∴令x=0，则y=4，
∴B（0，4）．

点评：本题考查了待定系数法求解析式以及直线与坐标轴的交点坐标，是基础题，难度小．