题目内容
如图，△ABC中，BE⊥AC于E，AD⊥BC于D．求证：△CDE∽△CAB．考点：相似三角形的判定
专题：证明题
分析：判断出点A、B、D、E四点共圆，再根据圆内接四边形的一个外角等于与它不相邻的内角可得∠CDE=∠CAB，再根据两组角对应相等的两个三角形相似证明．
解答：证明：∵BE⊥AC于E，AD⊥BC，
∴点A、B、D、E四点共圆，
∴∠CDE=∠CAB，
又∵∠C=∠C，
∴△CDE∽△CAB．
∴点A、B、D、E四点共圆，
∴∠CDE=∠CAB，
又∵∠C=∠C，
∴△CDE∽△CAB．
点评：本题考查了相似三角形的判定，解题的关键在于考虑利用四点共圆求出∠CDE=∠CAB．
练习册系列答案
相关题目
已知六边形ABCDEF的每个角都相等，MN⊥DE，求证：MN⊥AB．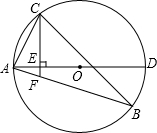
如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，作CE⊥AD，垂足为E，CE的延长线与AB交于F．试分析∠ACF与∠ABC是否相等，并说明理由．
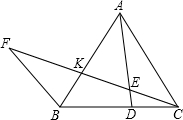如图，在等边△ABC中，K、D两点分别在AB、BC上，BK=CD，连接AD、CK并延长CK至点F，连接FB，∠F=30°．
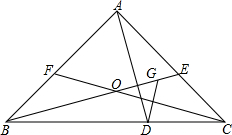如图，在等腰△ABC中，AB=AC，∠BAC=90°，AE=AF，BE、CF交于点O，过A作BE的垂线交BC于D，过D作CF的垂线交BE于G．