题目内容
已知a1,a2,…,a2004都是正数,如果M=(a1+a2+…+a2003)(a2+a3+…+a2004),N=(a1+a2+…+a2004)(a2+a3+…+a2003),那么M、N的大小关系是( )
| A、M>N | B、M<N |
| C、M=N | D、不确定的 |
考点:整式的混合运算
专题:换元法
分析:设S=a2+a3+…+a2003,表示出M与N,利用作差法比较大小即可.
解答:解:设S=a2+a3+…+a2003,则M=(a1+S)(S+a2004)=a1S+Sa2004+S2+a1a2004,
N=(a1+S+a2004)S=a1S+Sa2004+S2,
∴M-N=a1•a2004>0(a1,a2,…,a2004都是正数),
∴M>N.
故选A
N=(a1+S+a2004)S=a1S+Sa2004+S2,
∴M-N=a1•a2004>0(a1,a2,…,a2004都是正数),
∴M>N.
故选A
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
如果以扇形的半径为直径作一个圆,这个圆的面积恰好与扇形的面积相等,则扇形圆心角的度数为( )
| A、60° | B、90° |
| C、120° | D、150° |
 如图,在?ABCD中,BM=MC,AM交BD于点N,则BN:ND的值是( )
如图,在?ABCD中,BM=MC,AM交BD于点N,则BN:ND的值是( )| A、1:2 | B、1:2 |
| C、1:3 | D、2:1 |
下列语句:
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
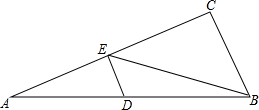 如图,在Rt△ABC中,∠C=90°,DE⊥AC于E,点D在线段AB上,已知AE=12,AD=13,CE=15,则AB=
如图,在Rt△ABC中,∠C=90°,DE⊥AC于E,点D在线段AB上,已知AE=12,AD=13,CE=15,则AB= 如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值.
如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值. 如图,△ABC中,BE⊥AC于E,AD⊥BC于D.求证:△CDE∽△CAB.
如图,△ABC中,BE⊥AC于E,AD⊥BC于D.求证:△CDE∽△CAB.