题目内容
在直角坐标系中,一次函数y=
x+2的图象与x轴交于点A,与y轴交于点B.在x轴上是否存在点P,使三角形PAB为等腰三角形?
| ||
| 3 |
考点:等腰三角形的判定,一次函数图象上点的坐标特征
专题:
分析:要在x轴上寻找点P,使△PAB为等腰三角形,需分情况讨论:①PB=AB=4时;②当PA=PB时;③当PA=PB=4,分别求得点P的坐标即可.
解答:解:分三种情况讨论:
①当PB=AB=4,点P和A关于y轴对称,则P1(2
,0);
②当PA=PB,利用两点间的距离公式可得(x+2
)2=x2+(0-2)2,解得P2(-
,0);
③当PA=PB=4,则P3(4-2
,0),P4(4-2
,0).
综上所述,存在满足条件的点P1(2
,0);P2(-
,0);P3(4-2
,0),P4(4-2
,0).
①当PB=AB=4,点P和A关于y轴对称,则P1(2
| 3 |
②当PA=PB,利用两点间的距离公式可得(x+2
| 3 |
| 2 |
| 3 |
| 3 |
③当PA=PB=4,则P3(4-2
| 3 |
| 3 |
综上所述,存在满足条件的点P1(2
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了等腰三角形的判定以及一次函数图象上点的坐标特征,仔细分析题意,结合图形,利用相似三角形、分类讨论来解决问题.

练习册系列答案
相关题目
小明使用电脑编了如下一个程序:
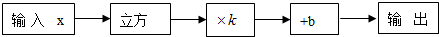
已知当输入x的值是2时,输出的值为-14,当输入x的值是-2时,输出的值为18,则当输入x的值为
时,输出的值为( )
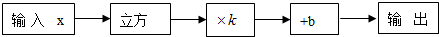
已知当输入x的值是2时,输出的值为-14,当输入x的值是-2时,输出的值为18,则当输入x的值为
| 1 |
| 2 |
A、1
| ||
B、-1
| ||
C、1
| ||
D、1
|
 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两个都不同行且不同列的概率为
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两个都不同行且不同列的概率为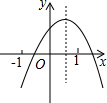 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.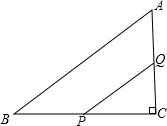 如图,在△ABC中,∠C=90°,BC=8cm,tanB=
如图,在△ABC中,∠C=90°,BC=8cm,tanB=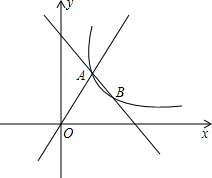 如图,直线y=3x与双曲线y=
如图,直线y=3x与双曲线y=