题目内容
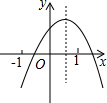 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.| A、一 | B、二 | C、三 | D、四 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得到a<0,由抛物线的对称轴位置得到b>0,由抛物线与y轴的交点位置得c>0,所以abc<0,观察函数图象得到x=1时,y>0,即a+b+c>0,然后根据第四象限点的坐标特征判断点(a+b+c,abc)所在象限.
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,所以A选项错误;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,
∴x=1时,y>0,
∴a+b+c>0,
∴点(a+b+c,abc)在第四象限.
故选D.
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,所以A选项错误;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,
∴x=1时,y>0,
∴a+b+c>0,
∴点(a+b+c,abc)在第四象限.
故选D.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
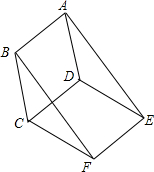 如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )
如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )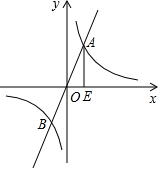 如图,已知函数y=2x图象和函数y=
如图,已知函数y=2x图象和函数y=