题目内容
8.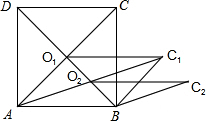 如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.
如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.
分析 设平行四边形ABC1O1的面积为S1,推出S△ABO1=$\frac{1}{2}$S1,又S△ABO1=$\frac{1}{4}$S正方形,推出S1=$\frac{1}{2}$S正方形=10=$\frac{10}{{2}^{0}}$;设ABC2O2为平行四边形为S2,由S△ABO2=$\frac{1}{2}$S2,又S△ABO2=$\frac{1}{8}$S正方形,推出S2=$\frac{1}{4}$S正方形=5=$\frac{10}{{2}^{1}}$,观察规律即可解决问题.
解答 解:∵设平行四边形ABC1O1的面积为S1,
∴S△ABO1=$\frac{1}{2}$S1,
又∵S△ABO1=$\frac{1}{4}$S正方形,
∴S1=$\frac{1}{2}$S正方形=10=$\frac{10}{{2}^{0}}$;
设ABC2O2为平行四边形为S2,
∴S△ABO2=$\frac{1}{2}$S2,
又∵S△ABO2=$\frac{1}{8}$S正方形,
∴S2=$\frac{1}{4}$S正方形=5=$\frac{10}{{2}^{1}}$;
…,
同理:设ABC6O6为平行四边形为S6,S6=$\frac{10}{{2}^{5}}$=$\frac{5}{16}$.
故答案为$\frac{5}{16}$.
点评 此题考查了矩形及平行四边形的性质,要求学生审清题意,找出面积之间的关系,归纳总结出一般性的结论.考查了学生观察、猜想、验证及归纳总结的能力.

练习册系列答案
相关题目
18.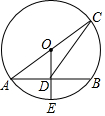 如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
 如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )
如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=$\frac{3}{2}$,则AB与DE的数量关系是( )| A. | AB=2DE | B. | AB=3DE | C. | AB=4DE | D. | 2AB=3DE |
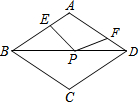 如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为3.
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为3. 已知:△ABC为等腰直角三角形,AB=AC=2,GA=CD=1,连接BD,过点A向BD作垂线,交BC于点F,BD于点E,连接CF,求证:∠G=∠D.
已知:△ABC为等腰直角三角形,AB=AC=2,GA=CD=1,连接BD,过点A向BD作垂线,交BC于点F,BD于点E,连接CF,求证:∠G=∠D.