题目内容
13. 已知:△ABC为等腰直角三角形,AB=AC=2,GA=CD=1,连接BD,过点A向BD作垂线,交BC于点F,BD于点E,连接CF,求证:∠G=∠D.
已知:△ABC为等腰直角三角形,AB=AC=2,GA=CD=1,连接BD,过点A向BD作垂线,交BC于点F,BD于点E,连接CF,求证:∠G=∠D.
分析 作AM⊥BC于M交BD于N.首先证明△ABN≌△CAF,推出AN=CF,再证明△GCF≌△DAN,即可解决问题.
解答 证明:作AM⊥BC于M交BD于N.
∵AB=AC,AM⊥BC,
∴∠ABC=∠MAC=∠ACB=45°,
∵∠FMA=∠FEB=90°,∠AFM=∠BFE,
∴∠FBE=∠FAM,
∴∠NBA=∠FAC,
在△ABN和△CAF中,
$\left\{\begin{array}{l}{∠BAN=∠ACF}\\{AB=AC}\\{∠ABN=∠CAF}\end{array}\right.$,
∴△ABN≌△CAF,
∴AN=CF,
∵AG=CD=1,
∴CG=AD,
在△GCF和△DAN中,
$\left\{\begin{array}{l}{CF=AN}\\{∠GCF=∠DAN}\\{CG=AD}\end{array}\right.$,
∴△GCF≌△DAN,
∴∠G=∠D.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
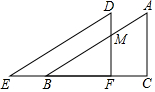 如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.
如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.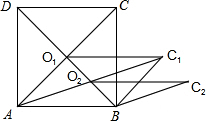 如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.
如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.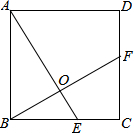 如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.
如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.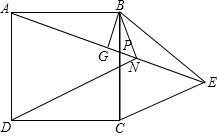 如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.
如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.