题目内容
16.已知矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=2cm,则该矩形的面积为$\sqrt{3}$cm2.分析 根据∠AOD=120°,可得∠AOB=60°,则△AOB为等边三角形,由AC的长可得AB的长,由勾股定理得BC的长,再求出矩形的面积即可.
解答 解:∵∠AOD=120°,可得∠AOB=60°,
∵AO=BO=CO=DO,AC=2cm,
∴AB=1cm,
∵∠ABC=90°,
∴∠ACB=30°,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{3}$cm,
∴矩形的面积=1×$\sqrt{3}$=$\sqrt{3}$cm2.
故答案为:$\sqrt{3}$cm2.
点评 本题考查了矩形的对角线平分且相等的性质,注意勾股定理的熟练应用是解题的关键.

练习册系列答案
相关题目
6.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
11.要了解某市九年级学生的视力状况,从中抽查了500名学生的视力状况,那么样本是指( )
| A. | 某市所有的九年级学生 | B. | 某市所有的九年级学生的视力状 | ||
| C. | 被抽查的500名九年级学生 | D. | 被抽查的500名学生的视力状况 |
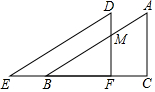 如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.
如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.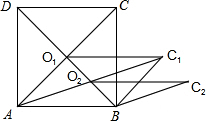 如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.
如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.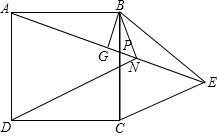 如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.
如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.