题目内容
20.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1看作一个整体,然后设x2-1=y…①,
那么原方程可化为y2-5y+4=0,解得y1=1,y2=4
当y=1时,x2-1=1,∴x2=2,∴x=±$\sqrt{2}$
当y=4时,x2-1=4,∴x2=5,∴x=±$\sqrt{5}$
故原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\sqrt{5}$,x4=-$\sqrt{5}$
上述解题过程中,将原方程中某个多项式视为整体,并用另一个未知数替换这个整体,从而把高次方程化为低次方程,实现降次的目的,这种解方程的方法称为“换元法”
解答问题:请用换元法解方程x2-2x+$\frac{21}{{x}^{2}-2x}$=10.
分析 设t=x2-2x,用t代替方程中的(x2-2x),然后解关于t的分式方程,然后再来求关于x的一元二次方程.
解答 解:设t=x2-2x,
依题意得:t+$\frac{21}{t}$=10,
t2-10t+21=0,
(t-3)(t-7)=0,
则t=3或t=7.
经检验,t=3或t=7都是所列方程的解.
①当t=3时,x2-2x=3,
整理,得
(x+3)(x-1)=0,
解得x1=-3,x2=1;
②当t=7时,x2-2x=7,
x2-2x-7=0.
解得x=$\frac{2±4\sqrt{2}}{2}$=1±2$\sqrt{2}$.
综上所述,x1=-3,x2=1,x3=1+2$\sqrt{2}$,x4=1-2$\sqrt{2}$.
点评 本题考查了换元法解一元二次方程和分式方程,注意,解分式方程时要验根.

练习册系列答案
相关题目
10.计算
(1)3a•(-2a2)+a3
(2)(-1)2015+(π-3.14)0+(-$\frac{1}{2}$)-2
(3)-2x2y(3x2-2x-3)
(4)(x+2)(x-1)-3x(x+1)
(1)3a•(-2a2)+a3
(2)(-1)2015+(π-3.14)0+(-$\frac{1}{2}$)-2
(3)-2x2y(3x2-2x-3)
(4)(x+2)(x-1)-3x(x+1)
11.要了解某市九年级学生的视力状况,从中抽查了500名学生的视力状况,那么样本是指( )
| A. | 某市所有的九年级学生 | B. | 某市所有的九年级学生的视力状 | ||
| C. | 被抽查的500名九年级学生 | D. | 被抽查的500名学生的视力状况 |
15.2sin45°的值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{2}$ | D. | 3 |
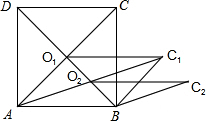 如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.
如图,正方形ABCD的长为2$\sqrt{5}$cm,对角线交于点O1,以AB,AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,依此类推,则平行四边形AO6C6B的面积为$\frac{5}{16}$cm2.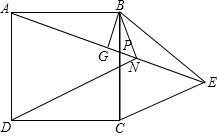 如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.
如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.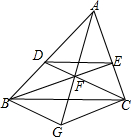 如图,在△ABC中,D、E分别在AB、AC上,并且DE∥BC,BE和CD交于点F,过点C点引CG∥EB,交AF的延长线于G,连接BG.求证:
如图,在△ABC中,D、E分别在AB、AC上,并且DE∥BC,BE和CD交于点F,过点C点引CG∥EB,交AF的延长线于G,连接BG.求证: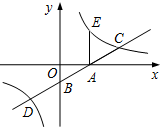 如图所示,直线y=$\frac{\sqrt{3}}{3}x-\sqrt{3}$与x、y轴分别交于A、B,与反比例函数$y=\frac{k}{x}$(k>0)的图象交于点C,过点A作x轴的垂线交该反比例函数图象于点E.
如图所示,直线y=$\frac{\sqrt{3}}{3}x-\sqrt{3}$与x、y轴分别交于A、B,与反比例函数$y=\frac{k}{x}$(k>0)的图象交于点C,过点A作x轴的垂线交该反比例函数图象于点E.