题目内容
9.一个不透明的纸盒中装有大小相同的黑、白两种颜色的小球,其中白球3个(分别用白1、白2、白3表示),若从中任意摸出一个小球,是白球的概率为$\frac{3}{4}$.(1)则纸盒中黑球的个数是1;
(2)第一次任意摸出一个小球,放回后第二次再摸出一个小球,请用树状图或列表的方法,求两次摸到相同颜色小球的概率.
分析 (1)由一个不透明的纸盒中装有大小相同的黑、白两种颜色的小球,其中白球3个,若从中任意摸出一个小球,是白球的概率为$\frac{3}{4}$,利用概率公式即可求得纸盒中球的个数,继而求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸到相同颜色小球的情况,再利用概率公式即可求得答案.
解答 解:(1)∵一个不透明的纸盒中装有大小相同的黑、白两种颜色的小球,其中白球3个,从中任意摸出一个小球,是白球的概率为$\frac{3}{4}$,
∴纸盒中共有球:3÷$\frac{3}{4}$=4(个),
∴纸盒中黑球的个数是:4-3=1(个).
故答案为:1.
(2)画树状图得:
∵共有16种等可能的结果,两次摸到相同颜色小球的有10种情况,
∴两次摸到相同颜色小球的概率为:$\frac{10}{16}$=$\frac{5}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.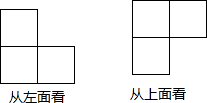 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.| A. | 4个 | B. | 5个 | C. | 6个 | D. | 无法确定 |
1. 如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
 如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )| A. | 24cm | B. | 20cm | C. | 12cm | D. | 8cm |
 如图,数学课上老师让同学们想办法测量学校国旗旗杆的高度,小明在阳光下走进旗杆的影子里,使自己的影子刚好被旗杆的影子遮住,已知小明的身高CD=1.70m,影长PD=2.2m,小明距旗杆底部的距离是19.8m,你能求出旗杆的高度AB吗?
如图,数学课上老师让同学们想办法测量学校国旗旗杆的高度,小明在阳光下走进旗杆的影子里,使自己的影子刚好被旗杆的影子遮住,已知小明的身高CD=1.70m,影长PD=2.2m,小明距旗杆底部的距离是19.8m,你能求出旗杆的高度AB吗?


