题目内容
20.过等腰Rt△ABC的直角顶点C作直线l,过A、B分别作AD⊥l于D,BE⊥l于E点,已知AD=5,BE=3,则DE的长为2.分析 证明△ACD≌△CBE,得出AD=CE,BE=CD,从而得到DE=AD-BE或DE=AD+BE.
解答 解:若A、B在直线l的异侧,如图: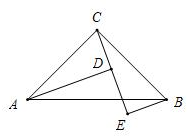
∵AD⊥CE,BE⊥CE,
∴∠CAD+∠DCA=90°,∠CBE+∠ECB=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACD=∠CBE}\\{∠ADC=∠CEB}\end{array}\right.$,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE-CD=AD-BE=2;
若A、B在直线l的同侧,如图: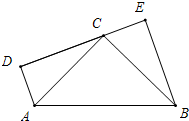
同理可证得:DE=AD+BE=8;
故答案为2或8.
点评 本题考查全等三角形的判定与性质,难度虽然不大,但本题所呈现的图形却是一个经常出现的经典模型,需要牢固掌握.掌握好全等三角形的判定方法是基本要求和解答的关键,同时注意考虑两种情况.

练习册系列答案
相关题目
15.已知一个等腰三角形两内角的度数之比为1:2,则这个等腰三角形底角的度数为( )
| A. | 72° | B. | 45° | C. | 45°或72° | D. | 60° |
12.若m2=2且m<0,则m的范围( )
| A. | 0<m<1 | B. | -1<m<0 | C. | -2<m<-1 | D. | -3<m<-2 |
 在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,若∠AED=60°,∠EDC=100°,则∠ADE=50°.
在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,若∠AED=60°,∠EDC=100°,则∠ADE=50°.