题目内容
抛物线y=mx2+(2m+1)x+m+1的图象与x轴的交点的个数为( )
| A、2 | B、1 | C、0 | D、0,1或2 |
考点:抛物线与x轴的交点
专题:
分析:先令mx2+(2m+1)x+m+1=0求出△的值,再判断出△的符号即可.
解答:解:令mx2+(2m+1)x+m+1=0,
∵△=(2m+1)2-4m(m+1)=1>0,
∴抛物线y=mx2+(2m+1)x+m+1的图象与x轴有两个不同的交点.
故选A.
∵△=(2m+1)2-4m(m+1)=1>0,
∴抛物线y=mx2+(2m+1)x+m+1的图象与x轴有两个不同的交点.
故选A.
点评:本题考查的是抛物线与x轴的交点,熟知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0的关系是解答此题的关键.

练习册系列答案
相关题目
若m是方程x2-2014x-1=0的根,则(m2-2014m+3)(m2-2014m+4)的值为( )
| A、16 | B、12 | C、20 | D、30 |
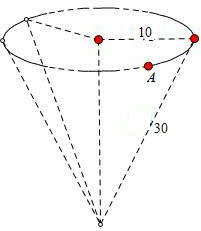 圆锥底面半径OA=10,母线=30,一只蚂蚁从A点出发,绕侧面一周回到A点,最短路径是多少?
圆锥底面半径OA=10,母线=30,一只蚂蚁从A点出发,绕侧面一周回到A点,最短路径是多少?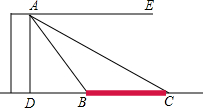 如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)
如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)