题目内容
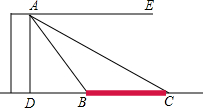 如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)
如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:在直角△ABD中首先求得∠DAB,然后利用三角函数求得BD的长,然后在直角△ADC中,利用三角函数求得DC,根据BC=DC-BD即可求解.
解答:解:在直角△ABD中,∠DAB=90°-∠EAB=90°-60°=30°,
则BD=AD•tan∠DAB=30×
=10
≈17.32(cm),
在直角△ADC中,∠ACD=∠EAC=30°,
则DC=AD•cos5ACD=30
(cm),
则BC=DC-BD=30
-10
=20
≈34.64(cm).
则BD=AD•tan∠DAB=30×
| ||
| 3 |
| 3 |
在直角△ADC中,∠ACD=∠EAC=30°,
则DC=AD•cos5ACD=30
| 3 |
则BC=DC-BD=30
| 3 |
| 3 |
| 3 |
点评:本题考查了解直角三角形,正确理解方向角的定义,理解直角三角形中的边和角的关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y=mx2+(2m+1)x+m+1的图象与x轴的交点的个数为( )
| A、2 | B、1 | C、0 | D、0,1或2 |
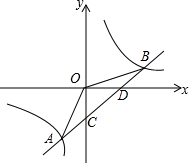 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=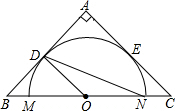 如图,在等腰Rt△ABC中,O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,若OD=3,则AC=
如图,在等腰Rt△ABC中,O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,若OD=3,则AC=