Question

15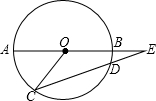．如图：AB为⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，已知AB=2DE，∠E=16°，则∠AOC的大小是48°．

Answer 1

分析 连结OD，如图，利用半径相等得到DE=DO，根据等腰三角形的性质得∠E=∠DOE=16°，则利用三角形外角性质可计算出∠CDO=32°，加上∠C=∠CDO=32°，然后再根据三角形外角性质可计算出∠AOC的度数．

解答 解：连结OD，如图，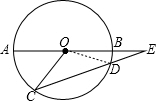
∵AB=2DE，
∴DE=DO，
∴∠E=∠DOE=16°，
∴∠CDO=∠E+∠DOE=32°，
∵OC=OD，
∴∠C=∠CDO=32°，
∴∠AOC=∠C+∠E=32°+16°=48°．
故答案为48．

点评 本题考查了圆的认识：圆可以看做是所有到定点O的距离等于定长r的点的集合；掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．