题目内容
20.计算:(1)$(\sqrt{12}-\sqrt{\frac{1}{3}})×\sqrt{3}$
(2)$\sqrt{8}$+$\sqrt{32}$-$\sqrt{2}$
(3)$\frac{{\sqrt{6}×\sqrt{3}}}{{\sqrt{2}}}$
(4)($\sqrt{3}$+$\sqrt{2}$)×($\sqrt{3}$-$\sqrt{2}$)
(5)$\sqrt{12}$-$\sqrt{27}$+$6\sqrt{\frac{1}{3}}$
(6)$\frac{{\sqrt{27}-\sqrt{12}}}{{\sqrt{3}}}$.
分析 (1)先进行二次根式的乘法运算,然后化简合并;
(2)先进行二次根式的化简,然后合并;
(3)先进行二次根式的乘法运算,然后化简;
(4)根据平方差公式求解;
(5)先进行二次根式的化简,然后合并;
(6)先进行二次根式的除法运算,然后合并.
解答 解:(1)原式=6-1
=5;
(2)原式=2$\sqrt{2}$+4$\sqrt{2}$-$\sqrt{2}$
=5$\sqrt{2}$;
(3)原式=$\sqrt{9}$
=3;
(4)原式=3-2
=1;
(5)原式=2$\sqrt{3}$-3$\sqrt{3}$+2$\sqrt{3}$
=-3$\sqrt{3}$;
(6)原式=3-2
=1.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简和合并.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.抛物线y=-(x+6)(x-4)的顶点坐标是( )
| A. | (-1,25) | B. | (-1,-25) | C. | (1,-21) | D. | (1,21) |
 如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.
如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.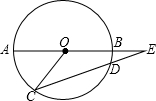 如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.
如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.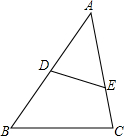 如图,DE与BC不平行,当$\frac{AB}{()}$=$\frac{()}{()}$时,△ABC与△ADE相似.
如图,DE与BC不平行,当$\frac{AB}{()}$=$\frac{()}{()}$时,△ABC与△ADE相似.