题目内容
3.已知:关于x的函数y=ax2+(2a+1)x+a的图象与x轴有且只有一个公共点,求实数a的值.分析 分类讨论:当a=0时,y=x,一次函数图象与x轴有且只有一个公共点;当a≠0时,抛物线y=ax2+(2a+1)x+a的图象与x轴有且只有一个公共点,根据判别式的意义得到△=(2a+1)2-4a2=0,然后解关于a的一次方程即可.
解答 解:当a=0时,y=x,此一次函数图象与x轴有且只有一个公共点;
当a≠0时,抛物线y=ax2+(2a+1)x+a的图象与x轴有且只有一个公共点,则△=(2a+1)2-4a2=0,解得a=-$\frac{1}{4}$,
综上所述,a的值为0或$-\frac{1}{4}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列计算各式:①-|-5|=5;②|a|=a;③-32=9;④(-2)2=4,其中正确的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.抛物线y=-(x+6)(x-4)的顶点坐标是( )
| A. | (-1,25) | B. | (-1,-25) | C. | (1,-21) | D. | (1,21) |
13.下列两项中,属于同类项的是( )
| A. | 62与x2 | B. | mn和-mn | C. | 0.2x2y与0.2xy2 | D. | 4ab与4abc |
 已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.
已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED. 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点. 如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.
如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.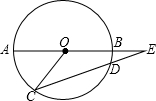 如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.
如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.