题目内容
7.观察下列各式:39×41=402-12
48×52=502-22
52×62=572-52
67×77=722-52,
请你把发现的规律用字母表示出来:mn=$(\frac{n+m}{2})^{2}$-$(\frac{n-m}{2})^{2}$.
分析 只需分别考虑被减数和减数的底数与积中的两个因素之间的关系,就可解决问题.
解答 解:39×41=402-12=($\frac{41+39}{2}$)2-($\frac{41-39}{2}$)2,
48×52=502-22=($\frac{52+48}{2}$)2-($\frac{52-48}{2}$)2,
52×62=572-52=($\frac{62+52}{2}$)2-($\frac{62-52}{2}$)2,
67×77=722-52=($\frac{77+67}{2}$)2-($\frac{77-67}{2}$)2,
…
由此可得:mn=${(\frac{n+m}{2})^2}-{(\frac{n-m}{2})^2}$.
故答案为${(\frac{n+m}{2})^2}-{(\frac{n-m}{2})^2}$.
点评 本题是规律探究题,主要考查了归纳探究的能力.

练习册系列答案
相关题目
16. 已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
 已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.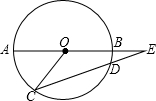 如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.
如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是48°.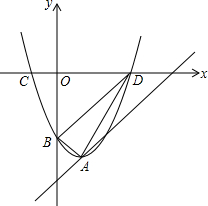 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上. 已知有理数a、b、c在数轴上的对应点如图所示,那么代数式|b-a|+|a+c|-|c-b|的化简结果是2a.
已知有理数a、b、c在数轴上的对应点如图所示,那么代数式|b-a|+|a+c|-|c-b|的化简结果是2a.