题目内容
17.已知矩形的一组邻边为3和4,那么这个矩形的对角线长是( )| A. | 7 | B. | 12 | C. | 5 | D. | 3.5 |
分析 根据矩形的性质得出∠B=90°,根据勾股定理求出AC即可.
解答 解:
∵四边形ABCD是矩形,
∴∠B=90°,AC=BD,
在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
即BD=AC=5,
故选C.
点评 本题考查了勾股定理,矩形的性质的应用,能熟记矩形的性质是解此题的关键,注意:矩形的四个角都是直角.

练习册系列答案
相关题目
8.在方程组$\left\{\begin{array}{l}{x+7y=m+1}\\{2x-y=4}\end{array}\right.$的解中,x,y的和等于2,则|2m+1|=( )
| A. | -3 | B. | 3 | C. | 0 | D. | 2 |
12.一元一次不等式-x-2<1-2x的正整数解有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
2.下列各组数中不能作为直角三角形的三边长的是( )
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 0.7,2.4,2.5 | C. | 6,8,10 | D. | 9,12,15 |
9.估算$\sqrt{30}-2$的值( )
| A. | 在1到2之间 | B. | 在2到3之间 | C. | 在3到4之间 | D. | 在4到5之间 |
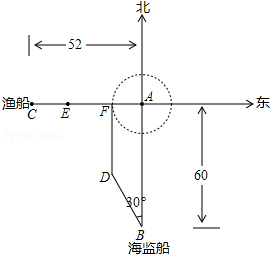 钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓 鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.
钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓 鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.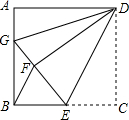 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( )