题目内容
3.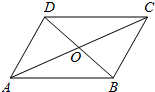 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF(1)根据题意,补全图形;
(2)求证:BE=DF.
分析 (1)如图所示;
(2)由全等三角形的判定定理SAS证得△BEO≌△DFO,得出全等三角形的对应边相等即可.
解答 (1)解:如图所示: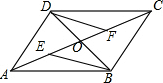
(2)证明:∵四边形ABCD是平行四边形,对角线AC、BD交于点O,
∴OB=OD,OA=OC.
又∵E,F分别是OA、OC的中点,
∴OE=$\frac{1}{2}$OA,OF=$\frac{1}{2}$OC,
∴OE=OF.
∵在△BEO与△DFO中,$\left\{\begin{array}{l}{OE=OF}&{\;}\\{∠BOE=∠DOF}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△BEO≌△DFO(SAS),
∴BE=DF.
点评 本题主要考查了全等三角形的判定与性质、平行四边形的性质的运用;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18. 为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
请根据所提供的信息解答下列问题:
(1)样本的中位数是44.5分;
(2)频率统计表中a=12,b=0.30;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
 为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:| 成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
| 成绩分组 | 频数 | 频率 |
| 35≤x<38 | 3 | 0.03 |
| 38≤x<41 | a | 0.12 |
| 41≤x<44 | 20 | 0.20 |
| 44≤x<47 | 35 | 0.35 |
| 47≤x≤50 | 30 | b |
(1)样本的中位数是44.5分;
(2)频率统计表中a=12,b=0.30;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论: 如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.
如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是16.