题目内容
15.已知数据x1,x2,x3,x4,x5的平均数是m,则数据x1+n,x2+n,x3+n,x4+n,x5+n的平均数是m+n.分析 本题需先根据要求的数分别列出式子,再根据x1,x2,x3,x4,x5的平均数是m,把它代入所求的式子,即可求出正确答案.
解答 解:这组数据x1+n,x2+n,x3+n,x4+n,x5+n的平均数是:
(x1+n+x2+n+x3+n+x4+n+x5+n)÷5
=[(x1+x2+x3+x4+x5)+(n+n+n+n+n)]÷5
根据x1,x2,x3,x4,x5的平均数是m,
∴(x1+x2+x3+x4+x5)÷5=m,
∴x1+x2+x3+x4+x5=5m,
把x1+x2+x3+x4+x5=5m代入[(x1+x2+x3+x4+x5)+(n+n+n+n+n)]÷5得;
=(5m+5n)÷5,
=m+n.
故答案为m+n.
点评 本题考查了算术平均数,在解题时要根据算术平均数的定义,再结合所给的条件是解本题的关键.

练习册系列答案
相关题目
6.下列事件中,是不可能事件的是( )
| A. | 抛掷2枚正方体骰子,都是6点朝上 | |
| B. | 任意画一个三角形,其内角和是360° | |
| C. | 通常加热到100℃时,水沸腾 | |
| D. | 经过有交通信号灯的路口,遇到红灯 |
10.某篮球队员共16人,每人投篮6次,投进球数的次数分配如表所示.
若此队投进球的中位数是2.5,则众数是2.
| 投进球数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 次数(人) | 1 | 2 | x | y | 3 | 2 | 2 |
4. 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )| A. | 2和1 | B. | 1.25和1 | C. | 1和1 | D. | 1和1.25 |
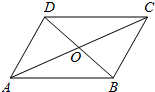 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF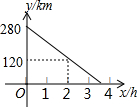 甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h
甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h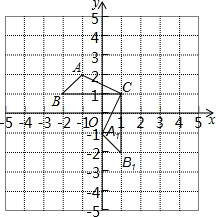 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(-1,2)、B(-2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(-1,2)、B(-2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).