题目内容
11.关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0.(1)试判断上述方程根的情况;
(2)若以上述方程的两个根分别为横坐标、纵坐标的点,恰在反比例函数y=$\frac{6}{x}$的图象上,求满足条件的k值.
分析 (1)表示出方程根的判别式,根据根的判别式的正负即可确定出方程根的情况;
(2)设方程的两根为x1,x2,根据题意得6=x1x2,再利用根与系数关系表示出x1x2,列出k关于k的一元二次方程,解方程即可.
解答 解:(1)∵△=b2-4ac=(2k+3)2-4×(k2+3k+2)=1>0,
∴方程有两个相等实数根;
(2)设方程x2-(2k+3)x+k2+3k+2=0的两个根为x1,x2,根据题意得6=x1x2,
又由一元二次方程根与系数的关系得x1x2=k2+3k+2,
∴6=k2+3k+2,
解得:k1=-4,x2=1,
∴满足条件的k值为-4或1.
点评 本题考查了一元二次方程根与系数的关系,根的情况判断,反比例函数的性质,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
6.下列事件中,是不可能事件的是( )
| A. | 抛掷2枚正方体骰子,都是6点朝上 | |
| B. | 任意画一个三角形,其内角和是360° | |
| C. | 通常加热到100℃时,水沸腾 | |
| D. | 经过有交通信号灯的路口,遇到红灯 |
16.五一期间刚到深圳的小明在哥哥的陪伴下,打算上午从莲山春早、侨城锦绣、深南溢彩中随机选择一个景点,下午从梧桐烟云、梅沙踏浪、一街两制中随机选择一个景点,小明恰好上午选中莲山春早,下午选中梅沙踏浪的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
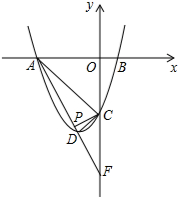 如图,已知抛物线y=ax2+bx+c与x轴交于点A、B(2,0),与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点.
如图,已知抛物线y=ax2+bx+c与x轴交于点A、B(2,0),与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点. 中缅边境实弹演习期间,空军战斗机随即将炮弹放在如图所示方格地面上(每个小方格都是边长相等的正方形),则炮弹落在阴影方格地面上的概率为$\frac{9}{25}$.
中缅边境实弹演习期间,空军战斗机随即将炮弹放在如图所示方格地面上(每个小方格都是边长相等的正方形),则炮弹落在阴影方格地面上的概率为$\frac{9}{25}$.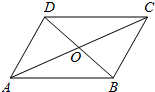 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF