题目内容
8.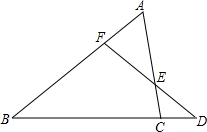 已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.
已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.
分析 过C作CG∥AB交DF于G,于是得到△CDG∽△BDF,△CEG∽△AFE,根据相似三角形的性质得到$\frac{CG}{BF}=\frac{CD}{BD}$,$\frac{CG}{AF}=\frac{CE}{AE}$,求得BF=4CG,AF=2CG,即可得到结论.
解答  解:过C作CG∥AB交DF于G,
解:过C作CG∥AB交DF于G,
∴△CDG∽△BDF,△CEG∽△AFE,
∴$\frac{CG}{BF}=\frac{CD}{BD}$,$\frac{CG}{AF}=\frac{CE}{AE}$,
∵BC=3CD,
∴$\frac{CD}{BD}$=$\frac{1}{4}$,
∴$\frac{CG}{BF}=\frac{CD}{BD}$=$\frac{1}{4}$,
∴BF=4CG,
∵AE=2EC,
∴$\frac{CG}{AF}=\frac{CE}{AE}$=$\frac{1}{2}$,
∴AF=2CG,
∴$\frac{AF}{BF}=\frac{2CG}{4CG}$=$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)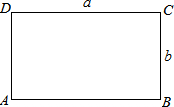 如图,长方形ABCD的长AB、宽CB分别为a米、b米,a、b满足2|a-4|+|b-2|=0,一动点P从A出发以1米/秒的速度沿A→D→C→B→A运动,另一动点Q从B出发以2米/秒的速度沿B→C→D→A→B运动,设P、Q同时出发,运动的时间为t.
如图,长方形ABCD的长AB、宽CB分别为a米、b米,a、b满足2|a-4|+|b-2|=0,一动点P从A出发以1米/秒的速度沿A→D→C→B→A运动,另一动点Q从B出发以2米/秒的速度沿B→C→D→A→B运动,设P、Q同时出发,运动的时间为t.