题目内容
16.已知抛物线y1=a(x-h)2+k与y2=x2+2x-8的开口方向和形状都相同,且抛物线y1的最低点的坐标是(-2,-1).(1)求抛物线y1对应的函数解析式;
(2)抛物线y1是由y2怎样平移得到的?
(3)求抛物线y1与x轴的两个交点的坐标.
分析 (1)由条件可以得出a=1,再将顶点坐标代入解析式就可以求出结论.
(2)由抛物线y2=x2+2x-8的顶点式即可求得顶点坐标,根据左加右减,上加下减可得出答案.
(3)令y1=0,得到关于x的方程,解方程即可求得.
解答 解:(1)∵抛物线y1=a(x-h)2+k与y2=x2+2x-8的开口方向和形状都相同,
∴a=1,
∵抛物线y1的最低点的坐标是(-2,-1).
∴抛物线y1对应的函数解析式y1=(x+2)2-1;
(2)由y2=x2+2x-8=(x+1)2-9可知,
抛物线y1是由y2向左平移一个单位,下平移8个单位平移得到的;
(3)令y=0,则x+2)2-1=0,
解得x1=-1,x2=-3,
所以,抛物线y1与x轴的两个交点的坐标为(-1,0),(-3,0).
点评 此题考查了待定系数法求二次函数解析式、图象的平移及抛物线与x轴的交点,掌握二次函数的顶点式y=a(x-h)2+k对应的开口方向、对称轴、顶点坐标是解题的关键.

练习册系列答案
相关题目
5.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的表达式;
(2)若A(-4,y1),B($\frac{11}{2}$,y2)两点都在该函数的图象上,试比较y1与y2的大小.
| x | … | -1 | 0 | 1 | 2 | 4 | … |
| y | … | 0 | -3 | -4 | -3 | 5 | … |
(2)若A(-4,y1),B($\frac{11}{2}$,y2)两点都在该函数的图象上,试比较y1与y2的大小.
 一块直角三角形木板的直角边BC长为1.5m,AB长为2m.要把它加工成一个面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图所示.请你用学过的知识说明哪位同学的加工方法符合要求.(加工损耗忽略不计)
一块直角三角形木板的直角边BC长为1.5m,AB长为2m.要把它加工成一个面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图所示.请你用学过的知识说明哪位同学的加工方法符合要求.(加工损耗忽略不计)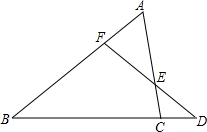 已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.
已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.