题目内容
14.解方程组:$\left\{\begin{array}{l}{x-y=4}\\{2x+y=2}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:由$\left\{\begin{array}{l}{x-y=4①}\\{2x+y=2②}\end{array}\right.$,
①+②得:3x=6,
解得:x=2,
把x=2代入①得:2-y=4,
解得:y=-2,
则原方程组的解为$\left\{{\begin{array}{l}{x=2}\\{y=-2}\end{array}}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
5.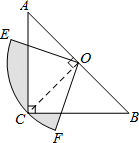 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )| A. | 2π-4 | B. | 4-π | C. | π-2 | D. | 4π-8 |
4.某工厂生产的一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长x(单位:cm)在5到50之间(含5和50),每张薄板的出场价y(单位:元)由基础价a和浮动价b两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价b与薄板的边长x成正比例.在营销过程中得到了表格中的数据.
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
| 薄板的边长x(cm) | 20 | 30 |
| 出厂价y(元/张) | 50 | 70 |
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?
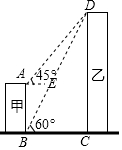 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号) 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.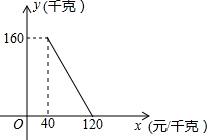 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示