题目内容

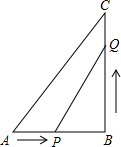如图所示，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从点A开始沿AB边向点B以1cm/s的速度运动，点Q同时从点B开始沿BC边向点C以2cm/s的速度运动．问：经过多少秒后，△PBQ的面积是△ABC的面积的三分之一？
考点：一元二次方程的应用
专题：几何动点问题
分析：设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出
解答：解：设经过x秒，△PBQ的面积等于8cm2则：
BP=6-x，BQ=2x，
所以S△PBQ=
1
2
×（6-x）×2x=8，
即x2-6x+8=0，
解得：x=2或4，
即经过2秒或4秒时，△PBQ的面积等于8cm2．
点评：本题主要是根据三角形的面积公式列出一元二次方程，关键是表示出PB和BQ的长．
练习册系列答案
相关题目
解方程：
（1）9-3y=5y+5
（2）4x-3（5-x）=6
（3）3x-[5-6（2-x）]=8            
（4）
1-m
2
-
3-3m
4
=1
（5）
2
7
(3y+7)=2-
3
2
y
（6）
x+1
0.2
+
2+3x
0.3
=1．
某地手机上网流量有两种收费方式：
方式一：5元包月，含30MB，若当月上网流量不超过30MB，不再收费；
若当月上网流量超过30MB，每超出1MB，加收0.5元；
方式二：10元包月，含70MB，若当月上网流量不超过70MB，不再收费；若当月上网流量超过70MB，每超出1MB，加收1元；
（1）某月某用户手机上网的流量为50MB，按方式一应支付的费用为
 
元；按方式二应支付的费用为
 
元；
（2）某月某用户手机上网的流量为80MB，按方式一应支付的费用为
 
元；按方式二应支付的费用为
 
元；
（3）当每月手机上网的流量为
 
MB时，两种方式支付的费用相等．
如图1，OC是∠AOB内的一条射线，
（1）将OB、OA向∠AOB内部翻折，使射线OA、OB都与射线OC重合；折痕分别为OE、OF，∠EOF=25°，求∠AOB的度数；
（2）如图2，∠MON=20°，OC是∠MON内部的一条射线，第一次操作分为两个步骤：第一步：将OC沿OM向∠MON外部翻折，得到OM1，第二步：将OC沿ON向∠MON外部翻折，得到ON1；第二次操作也分为两个步骤：第一步：将OC沿OM1向∠MON外部翻折，得到OM2；第二步：将OC沿ON1向∠MON外部翻折，得到ON2；…依此类推，在第
 
次操作的第
 
步恰好第一次形成一个周角，并求∠MOC的度数．
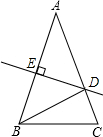如图，在△ABC中，AB=AC，AB的中垂线DE交AC于点D，交AB于点E，BC=10，△BDC的周长为22，求AB的值．
先化简，再求值：(a+b)(a-b)+20b(
b
2
-1)+6b(a+
10
3
)，其中a=
1
2
，b=-
1
3
．
（1）4x2-9=0．
（2）（x-2）2=9．
（3）2（x+1）3+16=0．
（1）已知32m=5，3n=10，求①9m-n；②92m-n．
（2）已知将（x3+mx+n）（x2-3x+4）展开的结果不含x3和x2项．
①求m、n的值；
②当m、n取第①小题的值时，求（m+n）（m2-mn+n2）的值．
计算与化简
（1）
3
x
-
6
1-x
-
x+5
x2-x
；
（2）
a2
a+1
-
1
a+1
；
（3）
1-
16
25
；
（4）
0.04
+
3-8
-
1
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网