题目内容
(1)已知32m=5,3n=10,求①9m-n;②92m-n.
(2)已知将(x3+mx+n)(x2-3x+4)展开的结果不含x3和x2项.
①求m、n的值;
②当m、n取第①小题的值时,求(m+n)(m2-mn+n2)的值.
(2)已知将(x3+mx+n)(x2-3x+4)展开的结果不含x3和x2项.
①求m、n的值;
②当m、n取第①小题的值时,求(m+n)(m2-mn+n2)的值.
考点:多项式乘多项式,幂的乘方与积的乘方,同底数幂的除法
专题:
分析:(1)根据幂的乘方和同底数幂的除法运算规则进行计算.
(2)①先利用多项式乘法法则把多项式展开,那么原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.由于展开后不含x3和x2项,则含x3和x2项的系数为0,由此可以得到4+m=0,-3m+n=0,解方程组即可以求出m、n.
②把m、n的值代入计算即可求解.
(2)①先利用多项式乘法法则把多项式展开,那么原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.由于展开后不含x3和x2项,则含x3和x2项的系数为0,由此可以得到4+m=0,-3m+n=0,解方程组即可以求出m、n.
②把m、n的值代入计算即可求解.
解答:解:(1)∵32m=5,3n=10,
∴9m=5,9n=100,
∴①9m-n;
=5÷100
=0.05;
②92m-n.
=25÷100
=0.25;
(2)①原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n
=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.
∵不含x3和x2项,
∴4+m=0,-3m+n=0,
解得m=-4,n=-12;
②当m=-4,n=-12时,
(m+n)(m2-mn+n2)
=(-4-12)×(16-48+144)
=-16×112
=-1792.
∴9m=5,9n=100,
∴①9m-n;
=5÷100
=0.05;
②92m-n.
=25÷100
=0.25;
(2)①原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n
=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.
∵不含x3和x2项,
∴4+m=0,-3m+n=0,
解得m=-4,n=-12;
②当m=-4,n=-12时,
(m+n)(m2-mn+n2)
=(-4-12)×(16-48+144)
=-16×112
=-1792.
点评:(1)考查幂的乘方和同底数幂的除法运算;幂的乘方:底数不变,指数相乘;同底数幂的除法:底数不变,指数相减.
(2)考查了多项式相乘法则以及多项式的项的定义.
(2)考查了多项式相乘法则以及多项式的项的定义.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
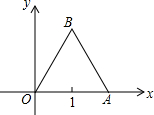 如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.
如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.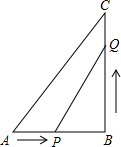 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q同时从点B开始沿BC边向点C以2cm/s的速度运动.问:经过多少秒后,△PBQ的面积是△ABC的面积的三分之一?
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q同时从点B开始沿BC边向点C以2cm/s的速度运动.问:经过多少秒后,△PBQ的面积是△ABC的面积的三分之一? 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值. 如图,点C、D为线段AB的三等分点,点E在线段DB上,若AB=9cm,BE=
如图,点C、D为线段AB的三等分点,点E在线段DB上,若AB=9cm,BE=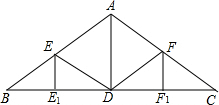 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.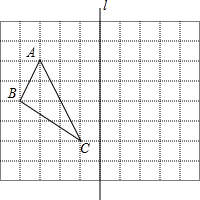 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上.请在网格中按要求作出下列图形,并标注相应的字母.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上.请在网格中按要求作出下列图形,并标注相应的字母.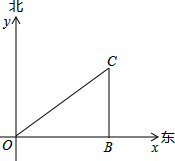 2012年4月中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
2012年4月中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).