题目内容
如图1,OC是∠AOB内的一条射线,
(1)将OB、OA向∠AOB内部翻折,使射线OA、OB都与射线OC重合;折痕分别为OE、OF,∠EOF=25°,求∠AOB的度数;
(2)如图2,∠MON=20°,OC是∠MON内部的一条射线,第一次操作分为两个步骤:第一步:将OC沿OM向∠MON外部翻折,得到OM1,第二步:将OC沿ON向∠MON外部翻折,得到ON1;第二次操作也分为两个步骤:第一步:将OC沿OM1向∠MON外部翻折,得到OM2;第二步:将OC沿ON1向∠MON外部翻折,得到ON2;…依此类推,在第 次操作的第 步恰好第一次形成一个周角,并求∠MOC的度数.
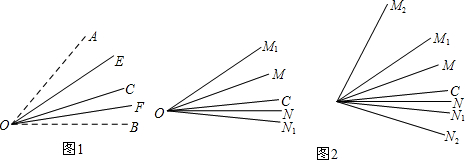
(1)将OB、OA向∠AOB内部翻折,使射线OA、OB都与射线OC重合;折痕分别为OE、OF,∠EOF=25°,求∠AOB的度数;
(2)如图2,∠MON=20°,OC是∠MON内部的一条射线,第一次操作分为两个步骤:第一步:将OC沿OM向∠MON外部翻折,得到OM1,第二步:将OC沿ON向∠MON外部翻折,得到ON1;第二次操作也分为两个步骤:第一步:将OC沿OM1向∠MON外部翻折,得到OM2;第二步:将OC沿ON1向∠MON外部翻折,得到ON2;…依此类推,在第

考点:角的计算
专题:规律型
分析:(1)利用翻折变换的性质得出∠AOE=∠EOC,∠COF=∠FOB,进而得出∠AOB的度数;
(2)∠MOC=x°,20°翻折的40°再翻折…得到周角为360°,列出方程即可解答.
(2)∠MOC=x°,20°翻折的40°再翻折…得到周角为360°,列出方程即可解答.
解答:解:(1)∵将OB、OA向∠AOB内部翻折,使射线OA、OB都与射线OC重合;
折痕分别为OE、OF,∠EOF=25°,
∴∠AOB=2∠COE+2∠COF=2(∠EOC+∠COF)=50°;
(2)第五次;第一步;
设∠MOC=x°,
则16×20°+4x=360°,
解得:x=2.5,
所以∠MOC=2.5°;
折痕分别为OE、OF,∠EOF=25°,
∴∠AOB=2∠COE+2∠COF=2(∠EOC+∠COF)=50°;
(2)第五次;第一步;
设∠MOC=x°,
则16×20°+4x=360°,
解得:x=2.5,
所以∠MOC=2.5°;
点评:考查了角的计算,此题第一问难度小,易得出答案.第二问要利用规律作答,找出规律即可,对于学生而言,要善于发现规律,抽象出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,A、B、C、D是⊙O上的四点,若∠ACD=30°,则∠ABD等于( )
如图,A、B、C、D是⊙O上的四点,若∠ACD=30°,则∠ABD等于( )| A、20° | B、60° |
| C、30° | D、50° |
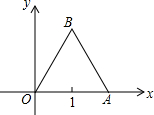 如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.
如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.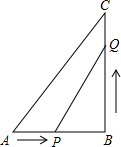 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q同时从点B开始沿BC边向点C以2cm/s的速度运动.问:经过多少秒后,△PBQ的面积是△ABC的面积的三分之一?
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q同时从点B开始沿BC边向点C以2cm/s的速度运动.问:经过多少秒后,△PBQ的面积是△ABC的面积的三分之一? 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值.