题目内容
4.已知正六边形的两条对边相距20cm,则它的边长是$\frac{20\sqrt{3}}{3}$cm.分析 根据正六边形的性质求出∠ABC的度数,连接AC,过B作BD⊥AC于点D,根据等腰三角形的性质得出AD=AC,求出∠ABD的度数,再根据锐角三角函数的定义即可得出AB的长.
解答 解: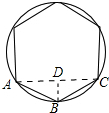 如图,连接AC,作BD⊥AC于D,
如图,连接AC,作BD⊥AC于D,
∴AD=CD=10cm,
∠ABC=$\frac{(6-2)×180°}{6}$=120°,
∴∠A=30°,
cosA=$\frac{AD}{AB}$,即$\frac{10}{AB}$=$\frac{\sqrt{3}}{2}$,
解得,AB=$\frac{20\sqrt{3}}{3}$,
故答案为:$\frac{20\sqrt{3}}{3}$cm.
点评 本题考查的是正多边形和圆的知识,掌握正多边形的性质和n边形内角和等于(n-2)×180°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.汤姆在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表:
(1)汤姆以折扣价购买商品A、B是第几次购物?为什么;
(2)求商品A、B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
| 商品A的数量(个) | 商品B的数量(个) | 总费用(元) | |
| 第一次购物 | 5 | 3 | 810 |
| 第二次购物 | 4 | 5 | 960 |
| 第三次购物 | 8 | 9 | 1080 |
(2)求商品A、B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
 如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.
如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度. 如图所示,AB=BE,CB=BD,∠1=∠2.求证:∠A=∠E.
如图所示,AB=BE,CB=BD,∠1=∠2.求证:∠A=∠E.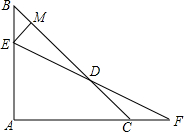 如图,AB=AC,∠A=90°,点E在AB上,点F在AC的延长线上,且BE=CF,EF交直线BC于D,过E点作EM⊥BC,垂足为M,试探究DM与BC之间存在怎样的数量关系?并给予证明.
如图,AB=AC,∠A=90°,点E在AB上,点F在AC的延长线上,且BE=CF,EF交直线BC于D,过E点作EM⊥BC,垂足为M,试探究DM与BC之间存在怎样的数量关系?并给予证明. 如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.
如图,在等腰△ABC中,AB=AC,分别作CD⊥AB,BE⊥AC,EG⊥AB,DF⊥AC.求证:四边形MDNE是菱形.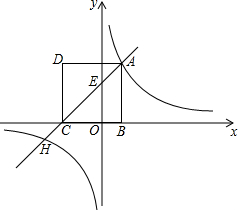 如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H.
如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H.