题目内容
14. 如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.
如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,则∠DAE=15度.
分析 由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD,然后根据∠DAE=∠BAE-∠BAD求解.
解答 解:在△ABC中,
∵∠BAC=180°-∠B-∠C=60°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=30°.
又∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°-∠B=15°,
∴∠DAE=∠BAE-∠BAD=15°.
故答案是:15.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
4.若-x3ym与xny是同类项,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.在函数y=$\frac{\sqrt{1-x}}{x-1}$中,自变量x的取值范围是( )
| A. | x≠1 | B. | x≤1 | C. | x<1 | D. | x≥1 |
6.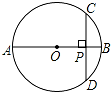 如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )
如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )
 如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )
如图,AB是⊙O的直径,弦CD⊥AB,CD=10,AP:PB=5:1,⊙O的半径是( )| A. | 6 | B. | $5\sqrt{5}$ | C. | 8 | D. | $3\sqrt{5}$ |
3.在有理数:-2,-(-2),|-2|,-|-2|中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
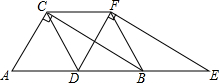 两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF沿射线AB方向平移,当D点移动到AB的中点时,