Question

9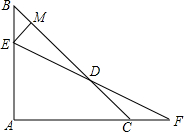．如图，AB=AC，∠A=90°，点E在AB上，点F在AC的延长线上，且BE=CF，EF交直线BC于D，过E点作EM⊥BC，垂足为M，试探究DM与BC之间存在怎样的数量关系？并给予证明．

Answer 1

分析 过D点作DH∥AC交AB于点H，由EH∥AC得到∠BEH=90°，又因为AB=AC，得出∠ACB=∠B=45°，证得BE=EH，EM⊥BC，得出BM=MH，证明△DEH≌△CDF，得到HE=CF，HD=HC，所以DM=DH+MH=$\frac{1}{2}$AB，即可求解．

解答 解：如图，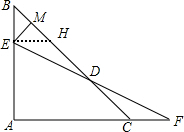

过D点作DH∥BC交AB于点H，
∴∠HED=∠F，
∵∠A=90°，AB=AC，
∴∠BEH=90°，∠ACB=∠B=45°，
∴BE=EH，
∵EM⊥BC，
∴BM=MH，
∵BE=CF，
∴EH=CF，
在△DEH和△DFC中，
$\left\{\begin{array}{l}{∠HED=∠F}\\{∠EDH=∠FDC}\\{EH=FC}\end{array}\right.$，
∴△DEH≌△DFC，
∴DH=DC，
∴DM=DH+MH=$\frac{1}{2}$BC．

点评 本题考查了全等三角形的判定与性质以及等腰直角三角形的性质，作出辅助线构造三角形全等是解决问题的关键．