Question

20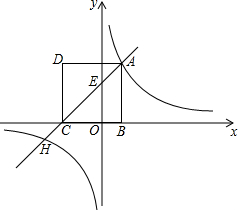．如图，已知四边形ABCD是正方形，边BC在x轴上，点A在反比例函数y=$\frac{4}{x}$的图象上，直线AC与y轴交于点E（0，3），与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H．
（1）求直线AC的函数解析式；
（2）求正方形ABCD边长的长；
（3）把直线AC沿x轴正方向平移6个单位，与x轴以及AB的延长线分别交于点F、G，点P是直线FG上的一个动点，当PH=AG时，求点P的坐标，并说明以A、G、P、H为顶点的四边形的形状．

Answer 1

分析 （1）根据相似三角形的判定与性质，可得OC的长，根据待定系数法，可得函数解析式；
（2）根据直线与双曲线，可得方程组，根据解方程组，可得答案；
（3）根据直线平移，可得FG的解析式，根据两点间距离，可得P点距离，根据平行四边形的判定，梯形的判定，可得答案．

解答 解：（1）由OC是正方形的对角线，得
BC=AB．
由OE∥AB，得
△COE∽△CBA，
OC=OE=3，
即C（-3，0），E（0，3），
AC的解析式为y=x+3；
（2）联立AC与反比例函数，得
$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=x+3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{y}_{2}=-1}\end{array}\right.$，
即A（1，4），H（-4，-1），
正方形ABCD边长为AB的长4；
（3）如图：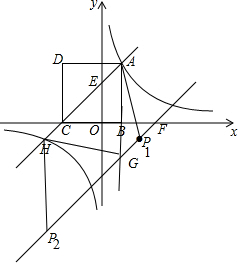

由平移，得
FG的解析式为y=x-3，
设P点坐标为（a，a-3），由PH=AG，得
（a+4）²+（a-2）²=[4-（-2）]²，
解得a=-4，a=2，即P₂（-4，-7），P₁（2，-1）．
当x=1时，y=1-3=-2，即G（1，-2），
当P₂（-4，-7）时，∵HP∥AG，AH∥PG，∴四边形AHPG是平行四边形；
当P₁（2，-1）时，∵AH∥PG，∴四边形AHGP是梯形．

点评 本题考查了反比例函数综合题，利用了相似三角形的判定与性质，待定系数法求函数解析式；解方程组求交点坐标，两点间的距离公式，平行四边形的判定，梯形的定义，分类讨论是解题关键，以防遗漏．