题目内容
15.同学们用气象探测气球探究气温与海拔高度的关系,1号气球从海拔5米处出发,以1米/分的速度匀速上升.与此同时,2号气球从海拔15米处出发,以0.5米/分的速度匀速上升.设1号、2号气球在上升过程中的海拔分别为y1(米)、y2(米),它们上升的时间为x(分),其中0≤x≤60.(1)填空:y1,y2与x之间的函数关系式分别为:
y1=x+5,y2=0.5x+15;
(2)当1号气球位于2号气球的下方时,求x的取值范围;当1号气球位于2号气球的上方时,求x的取值范围;
(3)设两个气球在上升过程中的海拔高度差为s(米).
请在A,B两题中任选一题解答,我选择A题.
A.直接写出当s=5时x的值.
B.直接写出当s>5时x的取值范围.
分析 (1)根据:上升过程中的海拔=起始位置海拔+上升的高度,分别列出函数关系式即可;
(2)根据(1)中两个函数关系式,根据位置的高低列出不等式,解不等式即可;
(3)海拔高度差s有2种可能,s=y1-y2、s=y2-y1,根据A、B两种情形列方程或不等式求解可得.
解答 解:(1)根据题意,y1=5+1•x=x+5,y2=15+0.5•x=0.5x+15;
(2)当y1<y2时,x+5<0.5x+15,
解得:x<20,
∵0≤x≤60,
∴当0≤x<20时,1号气球在2号气球的下方,
当y1>y2时,x+5>0.5x+15,
解得:x>20,
∵0≤x≤60,
∴当20<x≤60时,1号气球在2号气球的上方;
(3)A、根据题意,s=y1-y2=x+5-0.5x-15=0.5x-10,
若s=3,则0.5x-10=5,解得:x=30;
或s=y2-y1=0.5x+15-x-5=-0.5x+10,
若s=5,则-0.5x+10=5,解得:x=10;
故当s=5时,x的值为10或30;
B、当s>5时,①0.5x-10>5,解得:x>30;
②-0.5x+10>5,解得:x<10;
故当s>5时,0≤x<10或30<x≤60.
故答案为:(1)=x+5,=0.5x+15;(3)A.
点评 本题主要考查一次函数的实际应用能力,列出2函数关系式是基础和前提,根据位置的高低列出相应不等式是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.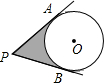 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
4. 汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )
汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )
①第3小时中的速度比第1小时中的速度快;
②第3小时中的速度比第1小时中的速度慢;
③第3小时后停止前进;
④第3小时后保持匀速前进.
 汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )
汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )①第3小时中的速度比第1小时中的速度快;
②第3小时中的速度比第1小时中的速度慢;
③第3小时后停止前进;
④第3小时后保持匀速前进.
| A. | ②③ | B. | ①③ | C. | ①④ | D. | ②④ |
5. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
 如图,C是∠AOB内部一点,D是∠AOB外部一点,在内部求作一点P,使PC=PD,并且使P点到∠AOB两边距离相等(保留作图痕迹).
如图,C是∠AOB内部一点,D是∠AOB外部一点,在内部求作一点P,使PC=PD,并且使P点到∠AOB两边距离相等(保留作图痕迹).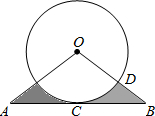 如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$.
如图,线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=3cm,AB=3$\sqrt{3}$cm,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}-\frac{3}{4}π$.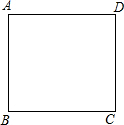 如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.
如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2. 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41) 如图,AB是⊙O的直径,过点B作BC⊥AB,过点A作AD∥OC交⊙O于点D,连结BD.若AB=6,BC=4,求AD的长.
如图,AB是⊙O的直径,过点B作BC⊥AB,过点A作AD∥OC交⊙O于点D,连结BD.若AB=6,BC=4,求AD的长.