题目内容
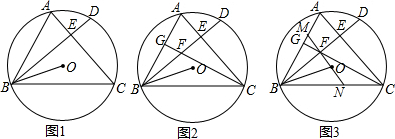
5.△ABC内接于⊙O,弦BD与AC相交于点E,连接BO,且∠OBC=∠ABD.(1)如图1,求证:AC⊥BD;
(2)如图2,在BE上取一点F,使EF=DE,直线CF与AB相交于点G,若∠ABC=60°.求证:BF=BO;
(3)如图3,在(2)的条件下,直线OF与AB相交于点M,与BC相交于点N,若NC=2MA,OB=2$\sqrt{7}$,求线段AE的长.
分析 (1)如图1,延长BO与⊙O相交于点K,连接CK,由已知条件和圆周角定理可证明∠ABE=∠BCK=90°,即AC⊥BE;
(2)延长CG与⊙O相交于点H,连接BH、OH,易证△OBH为等边三角形,由等边三角形的性质即可得到OB=BH=BF,问题得证;
(3)连接AO、CO.由(2)中的证明可知△BOH为等边三角形,所以BF=BO,由已知条件和全等三角形的判定方法可分别证明△BMF≌△BON,△AMO≌△ONC,进而可得AM=ON,MO=NC,所以可设AM=ON=MF=2a,则MN=6a=BM=BN,BC=10a,AB=AM+BM=8a,再根据勾股定理和∠FBG的正弦值即可求出线段AE的长.
解答 (1)证明:如图1,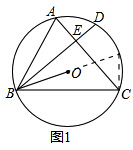
延长BO与⊙O相交于点K,连接CK.
∵BK为⊙O直径,
∴∠BCK=90°,
∵∠OBC=∠ABD,∠A=∠K,
∠AEB=∠180°-∠ABD-∠A=180°-∠OBC-∠K=∠BCK,
∴∠ABE=∠BCK=90°,
∴AC⊥BE;
(2)证明:如图2,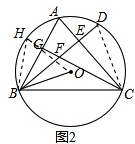
由(1)与已知可得AC垂直平分DF,
∴CD=CF,
∴∠DCA=∠ACF 且∠D=∠CFD,
延长CG与⊙O相交于点H,连接BH、OH.
∵弧AD=弧AD,
∴∠DCA=∠DBA.
∵弧AH=弧AH,
∴∠ACH=∠ABH,
∴∠ABH=∠ABD=∠OBC,
又∵∠BFH=∠CFD,
∴∠BGF=∠CEF=90°=∠BGH,
∴∠BHG=∠HFB,
∴BH=BF,
∵∠ABC=∠ABO+∠OBC=∠ABO+∠ABH=∠OBH=60°,OH=OB,
∴△OBH为等边三角形,
∴OB=BH=BF;
(3)解:连接AO、CO,如图3,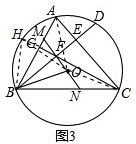
由(2)中的证明可知△BOH为等边三角形,BF=BO,
∴∠BFO=∠BOF,
∵∠BFO+∠BFM=180°,∠BOF+∠BON=180°
∴∠BFM=∠BON,
在△BMF和△BON中,
$\left\{\begin{array}{l}{∠MBF=∠NBO}\\{∠BFM=∠BON}\\{BF=BO}\end{array}\right.$,
∴△BMF≌△BON,
∴MF=ON,BM=BN,
∵∠MBN=60°,
∴△MBN是等边三角形,
∴∠BMN=∠BNM=60°,
∴∠AMN=∠CNM=120°,∠MAO+∠AOM=60°
∵∠AOC=2∠ABC=120°,
∴∠AOM+∠CON=60°,
∴∠AOM=∠OCN,
又∵AO=CO,
在△AMO和△ONC中,
$\left\{\begin{array}{l}{∠AMN=∠CNM}\\{∠AOM=∠CON}\\{OA=OC}\end{array}\right.$,
∴△AMO≌△ONC,
∴AM=ON,MO=NC,
设AM=ON=MF=2a,
∵NC=2MA,
∴MO=NC=4a,
∴OF=2a,MN=6a=BM=BN,BC=10a,AB=AM+BM=8a,
在Rt△MGF和Rt△BGC中,∠GMF=∠ABC=60°,
∴MG=$\frac{1}{2}$MF=a,GF=MFsin60°=$\sqrt{3}$a,BG=5a,
在Rt△BFG中,BF2=BG2+GF2=BO2,
∴(2$\sqrt{7}$)2=(5a)2+($\sqrt{3}$a)2,
∴a=1,
∴AB=8,GF=$\sqrt{3}$,
∵sin∠FBG=$\frac{GF}{BF}$=$\frac{\sqrt{3}}{2\sqrt{7}}$=$\frac{\sqrt{21}}{14}$,
在Rt△ABE中,sin∠FBG=$\frac{AE}{AB}$,
∴AE=AB•sin∠FBG=8×$\frac{\sqrt{21}}{14}=\frac{4\sqrt{21}}{7}$.
点评 本题考查了和圆有关的综合性题目,用到的知识点有垂径定理、圆周角定理、圆的内接三角形的有关性质、全等三角形的判定和性质、等边三角形的判定和性质、勾股定理的运用以及锐角三角函数的运用等知识点,题目的综合性较强,难度较大,对学生的运算能力要求较高,是一道非常不错的中考压轴题.

| 型号 | 数量(台) | 进价(元/台) |
| A | 10 | 150元 |
| B | 5 | 350元 |
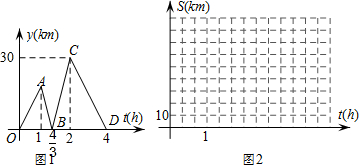
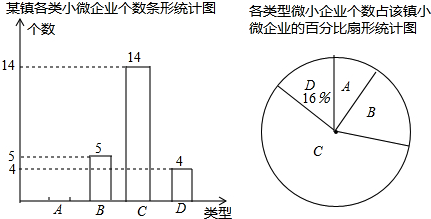
 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)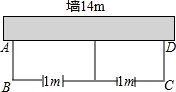 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.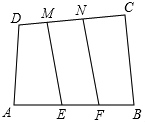 挑战极限:如图,已知四边形ABCD的面积为S,E、F为AB的三等分点,M、N为DC的三等分点.四边形EFNM的面积=$\frac{1}{3}$S.(选填“>”,“<”,“=”,“≤”,“≥”)
挑战极限:如图,已知四边形ABCD的面积为S,E、F为AB的三等分点,M、N为DC的三等分点.四边形EFNM的面积=$\frac{1}{3}$S.(选填“>”,“<”,“=”,“≤”,“≥”)