题目内容
9.计算与化简(1)(-2ab)+(-$\frac{1}{3}$a2b)+5ab-$\frac{1}{2}$a2b;
(2)计算:(-$\frac{5}{14}$)-2016$•(\frac{5}{14})^{2015}$;
(3)运用乘法公式计算:1232-122×124;
(4)(x-y+3)(x-y-3);
(5)先化简,再求值:(-$\frac{1}{5}$m3n4+$\frac{9}{10}$m2n3)÷(-$\frac{3}{5}$mn2),其中m=-2,n=$\frac{1}{2}$.
分析 (1)原式合并同类项即可得到结果;
(2)原式逆用积的乘方运算法则变形,计算即可得到结果;
(3)原式变形后,利用平方差公式计算即可得到结果;
(4)原式利用平方差公式及完全平方公式计算即可得到结果;
(5)原式利用多项式乘以单项式法则计算得到最简结果,把m与n的值代入计算即可求出值.
解答 解:(1)原式=3ab-$\frac{5}{6}$a2b;
(2)原式=(-$\frac{14}{5}$×$\frac{5}{14}$)2015×(-$\frac{14}{5}$)=-1×(-$\frac{14}{5}$)=$\frac{14}{5}$;
(3)原式=1232-(123-1)×(123+1)=1232-(1232-1)=1232-1232+1=1;
(4)原式=(x-y)2-9=x2-2xy+y2-9;
(5)原式=$\frac{1}{3}$m2n2-$\frac{3}{2}$mn,
当m=-2,n=$\frac{1}{2}$时,原式=$\frac{1}{3}$+$\frac{3}{2}$=1$\frac{5}{6}$.
点评 此题考查了整式的混合运算-化简求值,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.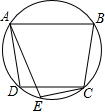 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )| A. | 110° | B. | 70° | C. | 80° | D. | 100° |
 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)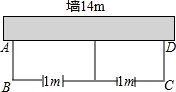 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门. 汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )
汽车行驶的路程与时间的关系如图所示,下列说法正确的是( )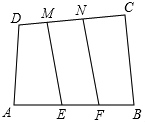 挑战极限:如图,已知四边形ABCD的面积为S,E、F为AB的三等分点,M、N为DC的三等分点.四边形EFNM的面积=$\frac{1}{3}$S.(选填“>”,“<”,“=”,“≤”,“≥”)
挑战极限:如图,已知四边形ABCD的面积为S,E、F为AB的三等分点,M、N为DC的三等分点.四边形EFNM的面积=$\frac{1}{3}$S.(选填“>”,“<”,“=”,“≤”,“≥”)
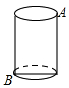 如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.
如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.