题目内容
16.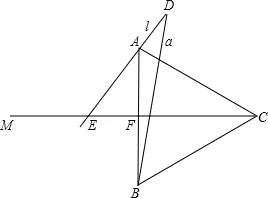 如图所示,已知正△ABC中射线CM⊥AB于F,射线BA绕B顺时针旋转,旋转后的射线记作a,同时线段AB所在直线绕A顺时针旋转,旋转后的直线记作直线l,当直线l旋转的角度是射线a旋转角度的4倍时,直线l于射线CM相交于E,与射线a相交于D,且∠D=30°.
如图所示,已知正△ABC中射线CM⊥AB于F,射线BA绕B顺时针旋转,旋转后的射线记作a,同时线段AB所在直线绕A顺时针旋转,旋转后的直线记作直线l,当直线l旋转的角度是射线a旋转角度的4倍时,直线l于射线CM相交于E,与射线a相交于D,且∠D=30°.(1)求射线a的旋转角是多少度;
(2)求证:DE=AB;
(3)探索:线段DE,EF,DB的数量关系.
分析 (1)根据三角形的一个外角等于与它不相邻的两内角的和,直线a,l的旋转角的关系建立方程4α=30°+α即可;
(2)由∠BCE=∠D=30°,判断出点B,C,D,E四点共圆,再判断出∠EBD=∠BDC,即可;
(3)判断出△BDE≌△ECA,再代换即可.
解答 解:(1)设直线l旋转角为α,
∴∠ABD=α
∵射线l旋转的角度是射线a旋转角度的4倍,
∴∠BAE=4α,
∵∠BAE=∠ABD+∠D,
∴4α=α+30°,
∴α=10°,
射线a的旋转角是10°;
(2)连接BE,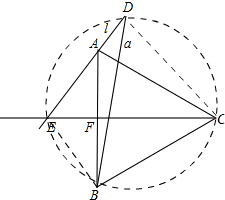
在正△ABC中,CF⊥AB,
∴∠BCE=30°,
∵∠D=30°,
∴∠BCE=∠D=30°,
∴点B,C,D,E四点共圆(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆)
∵CE⊥AB,AF=BF,
∴EA=EB,
∴∠EBA=∠BAE=40°,
∴∠EBD=50°,∠EBC=100°,
∴∠EDC=80°,
∴∠BDC=50°
∴∠EBD=∠BDC,
∴DE=BC,
∵BC=AB,
∴DE=AB,
(3)∵∠BAE=40°,
∴∠AEC=50°,
∵∠ABE=40°,∠ABD=10°,
∴∠EBD=∠AEC=50°
∵∠BDE=∠ACE=30°,DE=AC,
∴△BDE≌△ECA,
∴BD=EC=EF+FC=EF+$\frac{\sqrt{3}}{2}$AB=EF+$\frac{\sqrt{3}}{2}$DE.
点评 此题是几何变换综合题,主要考查了三角形全等的性质和判定,三角形的内外角的关系,四点共圆的判定,解本题的关键是说明点B,C,D,E四点共圆,也是本题的难点.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2÷a2=0 | C. | (2a)2=2a2 | D. | a•a2=a3 |
 已知:如图,正方形ABCD中,E为BD上一点,AE的延长线交CD于点F,交BC的延长线于点G,连结EC.
已知:如图,正方形ABCD中,E为BD上一点,AE的延长线交CD于点F,交BC的延长线于点G,连结EC.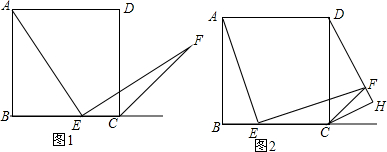
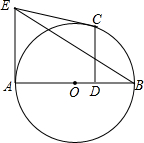 AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.
AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.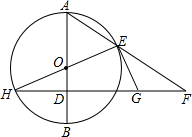 经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.
经过⊙O半径OB上一点D作直径AB的垂线交⊙O于点H,过直径HE的一端E作圆的切线交直线DH于G,延长AE交直线HD于点F.