题目内容
11.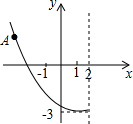 如图,二次函数y=ax2+bx+c的图象的一部分,已知A(-2.5,2),则根据图象可得到下列结论:
如图,二次函数y=ax2+bx+c的图象的一部分,已知A(-2.5,2),则根据图象可得到下列结论:①a>0,b2-4ac>0;
②x<m时,y随x的增大而减小,则m≤2;
③-2.5≤x<4时,-3≤y≤2;
④-3≤y≤0时,-1≤x≤5.
其中正确的序号是①②③.
分析 由抛物线的开口向上知a>0,图象与x轴有交点,可以推出b2-4ac>0,①正确;对称轴为x=2,可以推出x<m时,y随x的增大而减小,则m≤2,②正确;由A(-2.5,2)和顶点坐标(2,-3),可以推出-2.5≤x<4时,-3≤y≤2,③正确;由图象与x轴的交点横坐标x1<-1,x2>5,④错误.然后即可作出选择.
解答 解:①∵抛物线的开口向上,
∴a>0,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2-4ac>0,故正确;
②由图象可知对称轴为x=2,
∴在对称轴的左侧,y随x的增大而减小,
∴x<2时,y随x的增大而减小,则m≤2,正确;
③∵对称轴为x=2,
∴2-(-2.5)>4-2,
∴对于(-2.5,y1)、(4,y2),y1>y2,
∵顶点坐标为(2,-3),
∴-2.5≤x<4时,-3≤y≤2,正确;
④∵抛物线与x轴的交点横坐标x<-1或x>5,
∴-3≤y≤0时,-1≤x≤5,错误;
故正确的为①②③.
故答案为①②③.
点评 本题考查了二次函数的性质,解答本题关键是掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与x轴交点来确定.

练习册系列答案
相关题目
2.如图:在某地,人们发现某种蟋蟀1min所叫次数x与当地温度T之间的关系或为T=ax+b,下面蟋蟀所叫次数与温度变化情况对照表:
①根据表中的数据确定a、b的值;
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
| 蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
| 温度(℃)T | … | 15 | 17 | 20 | … |
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
20.不等式x-1≤1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
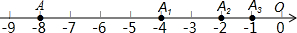 一条数轴如图所示,点A表示的数是-8.
一条数轴如图所示,点A表示的数是-8.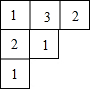 如图,是由若干个大小相同的正方体搭成的几何体的俯视图,其中小正方形中的数字表示该位置上的正方体的个数,则这个几何体的左视图是( )
如图,是由若干个大小相同的正方体搭成的几何体的俯视图,其中小正方形中的数字表示该位置上的正方体的个数,则这个几何体的左视图是( )