题目内容
14.(1)(x-y-z)(x-y+z);(2)($\frac{1}{3}$x+y)(-y+$\frac{1}{3}$x)($\frac{1}{9}$x2-y2);
(3)化简求值:a2(a+b)(a-b)-(2b-a2)(-2b+a2),其中a=2,b=$\frac{1}{2}$.
分析 (1)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
(2)原式利用平方差公式计算即可得到结果;
(3)原式利用平方差公式,完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)原式=(x-y)2-z2=x2-2xy+y2-z2;
(2)原式=($\frac{1}{9}$x2-y2)($\frac{1}{9}$x2-y2)=$\frac{1}{81}$x4-$\frac{2}{9}$x2y2+y4;
(3)原式=a4-a2b2+4b2-4ba2+a4=2a4-a2b2+4b2-4ba2,
当a=2,b=$\frac{1}{2}$时,原式=32-1+1-8=24.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.如图:在某地,人们发现某种蟋蟀1min所叫次数x与当地温度T之间的关系或为T=ax+b,下面蟋蟀所叫次数与温度变化情况对照表:
①根据表中的数据确定a、b的值;
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
| 蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
| 温度(℃)T | … | 15 | 17 | 20 | … |
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
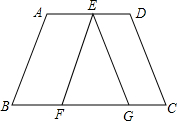 已知:如图,AB∥EF,CD∥EG,AD∥BC,∠A=125°,∠D=95°,求∠EFG、∠EGF、∠GEF的度数.
已知:如图,AB∥EF,CD∥EG,AD∥BC,∠A=125°,∠D=95°,求∠EFG、∠EGF、∠GEF的度数.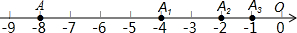 一条数轴如图所示,点A表示的数是-8.
一条数轴如图所示,点A表示的数是-8.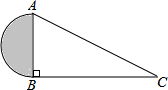 如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?
如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?