题目内容
1.求不定方程x2-5xy+6y2-3x+5y-11=0的整数解.分析 原方程变形为:(x-2y+1)(x-3y-4)=7,根据整数的整除性得到$\left\{\begin{array}{l}{x-2y+1=1}\\{x-3y-4=7}\end{array}\right.$;$\left\{\begin{array}{l}{x-2y+1=-1}\\{x-3y-4=-7}\end{array}\right.$;$\left\{\begin{array}{l}{x-2y+1=7}\\{x-3y-4=1}\end{array}\right.$;$\left\{\begin{array}{l}{x-2y+1=-7}\\{x-3y-4=-1}\end{array}\right.$;从而求得x,y的值.
解答 解:x2-5xy+6y2-3x+5y-11
=(x-2y)(x-3y)-3x+5y-11
=[(x-2y)+1][(x-3y)-4]-7
=(x-2y+1)(x-3y-4)-7
=0,
(x-2y+1)(x-3y-4)=7,
则$\left\{\begin{array}{l}{x-2y+1=1}\\{x-3y-4=7}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-22}\\{y=-11}\end{array}\right.$;
$\left\{\begin{array}{l}{x-2y+1=-1}\\{x-3y-4=-7}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$;
$\left\{\begin{array}{l}{x-2y+1=7}\\{x-3y-4=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=8}\\{y=1}\end{array}\right.$;
$\left\{\begin{array}{l}{x-2y+1=-7}\\{x-3y-4=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-30}\\{y=-11}\end{array}\right.$.
故不定方程x2-5xy+6y2-3x+5y-11=0的整数解为$\left\{\begin{array}{l}{x=-22}\\{y=-11}\end{array}\right.$;$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$;$\left\{\begin{array}{l}{x=8}\\{y=1}\end{array}\right.$;$\left\{\begin{array}{l}{x=-30}\\{y=-11}\end{array}\right.$.
点评 本题考查了非一次不定方程(组)中方程整数解的求法:把方程进行变形,使方程左边分解为含未知数的两个式子,右边为常数,然后利用整数的整除性求解.

| A. | 4 | B. | $\sqrt{34}$ | C. | 4或$\sqrt{34}$ | D. | 以上都不对 |
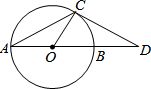 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°.判断DC是否为⊙O的切线,并说明理由.
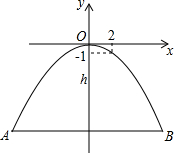 如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.
如图,桥拱是抛物线,上面有一点P,坐标是(2,-1),当水位线在AB位置时,A到B的水面宽为12m,求水面离桥顶的高度h.