题目内容
1．
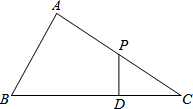如图，△ABC中，∠A=90°，P是AC的中点，PD⊥BC于D，BC=9，CD=3，求AB．
分析 利用两对角相等得到三角形相似得到三角形CDP与三角形CAB相似，由相似得比例，设PC=x，则有AC=2x，代入比例式求出x的值，即可确定出AB的长．
解答 解：∵∠PDC=∠BAC=90°，∠C=∠C，
∴△CDP∽△CAB，
∴$\frac{PC}{BC}$=$\frac{CD}{AC}$=$\frac{PD}{AB}$，
设PC=x，则有AC=2x，
∴$\frac{x}{9}$=$\frac{3}{2x}$，
解得：x=$\frac{3\sqrt{6}}{2}$，
∴AC=3$\sqrt{6}$，
根据勾股定理得：AB=$\sqrt{{8}^{2}-（3\sqrt{6}）^{2}}$=3$\sqrt{3}$．
点评 此题考查了相似三角形的判定与性质，勾股定理，熟练掌握相似三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
11．已知点A的坐标为（-2，3），点B的坐标为（0，1），则点A关于点B对称点的坐标为（ ）
| A． | （-2，2） | B． | （2，-3） | C． | （2，-1） | D． | （2，3） |
12．
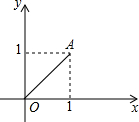如图，点A的坐标是（1，1），如果将线段OA绕点O按逆时针方向旋转135°，那么点A旋转后的对应点的坐标是（ ）
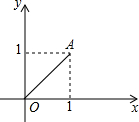如图，点A的坐标是（1，1），如果将线段OA绕点O按逆时针方向旋转135°，那么点A旋转后的对应点的坐标是（ ）| A． | （-$\sqrt{2}$，0） | B． | （0，-$\sqrt{2}$） | C． | （0，-1） | D． | （-1，0） |
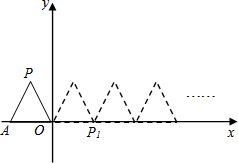如图，将边长为1的正三角形OAP沿x轴正方向连续翻转2013次，点P依次落在点P1，P2，P3…P2013的位置，则点P2013的横坐标为2012.5．
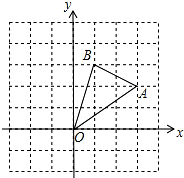如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．将△AOB绕点O逆时针旋转90°后得到△A1OB1．
将直角三角尺的顶点靠在直尺上，且斜边与这根直尺平行，那么在形成的这个图中（如图），与∠α互余的角共有2个．